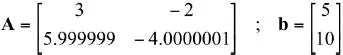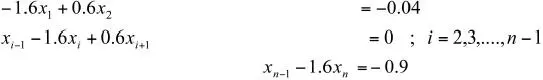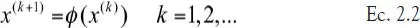Héctor Jorquera González - Métodos numéricos aplicados a Ingeniería

d) Ahora aplique las rutinas iterativas pcg, bicg, gmres, qmr, bicgstab en su forma más simple, es decir, utilizando como argumentos solamente la matriz Ay el vector boriginales. Calcule xy x 1para los casos en que se ingresa by b 1como vectores del lado derecho. ¿Qué resultados se obtienen? ¿Cómo se comparan estos resultados con los de las partes a) y b) anteriores? Nota: calcule los residuos de la solución x(o x 1) en cada caso.

e) Finalmente, concluya qué métodos de solución son más adecuados para abordar la resolución de este tipo de casos con matrices mal condicionadas.

10) Considere ahora el sistema lineal de ecuaciones A· x = bcon

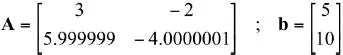
Repita el procedimiento del problema anterior, ahora usando b 1= [ 5.00004 ; 10.0003], etc.

11) El siguiente sistema tridiagonal de ecuaciones lineales representa las ecuaciones de un modelo simple de un proceso de extracción líquido-líquido, donde la composición x(i) de un soluto de interés cambia a lo largo de las n etapas de extracción (por ejemplo, el sulfato de cobre se extrae de una solución acuosa pobre en cobre y se concentra en una corriente de solvente orgánico).

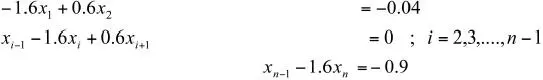
Tome n = 15 etapas y calcule el vector de concentraciones x. Grafíquelo usando plot(x).

Nota:

Para construir la matriz y el lado derecho del sistema de ecuaciones, se recomienda usar los comandos: zeros (n,1), ones (n,1) y spdiags . Emplee la función spy ( M) para verificar que la matriz Mposee una estructura tridiagonal.

1.5 Referencias

1. Moler, C. (2008). Numerical Computing with MATLAB. Disponible en la página web: http://www.mathworks.com/moler/; incluye una biblioteca de programas escritos en Matlab ®.

2. Wang, J.C. & Henke, G.E. (1966). Tridiagonal Matrix for Distillation. Hydrocarbon Process. Vol 45, N° 8, 155-163.

3. Hanna, O.W. & Sandall, O.C. (1995). Computational Methods in Chemical Engineering. Nueva Jersey: Prentice Hall.

4. Axelson, O. (1994). Iterative Solution Methods. Nueva York: Cambridge University Press.

5. Nakamura, S. (1992). Métodos numéricos aplicados con software México DF: Prentice Hall Hispanoamericana.

6. Gerald, C.F. Análisis numérico (2ª ed.). México DF: Alfaomega.

7. Sewell, G. (1988). The Numerical Solution of Ordinary and Partial Diferential Equations. Boston: Academic Press.

2. ECUACIONES NO LINEALES

Para resolver ecuaciones algebraicas en general se usan métodos iterativos de solución. Un método iterativo consta de las siguientes etapas:

i) Estimar un valor inicial para la solución buscada.

ii) Una fórmula para actualizar la solución aproximada que se obtiene.

iii) Un criterio para detener el proceso de actualización (chequeo de convergencia).

Notas:

a) Es importante distinguir entre el proceso (o algoritmo) iterativo completo y la fórmula de iteración (o de actualización).

b) La verificación del término “satisfactorio” del proceso es esencial y debe anticipar todas las posibles salidas del método iterativo. Debe ser capaz de notar cuando el algoritmo falla.

c) La etapa inicial requiere a menudo incluir pruebas para validar la consistencia de los datos iniciales (concentraciones positivas, etc.).

FIGURA 2.1. Diagrama de flujo típico de un proceso de iteración

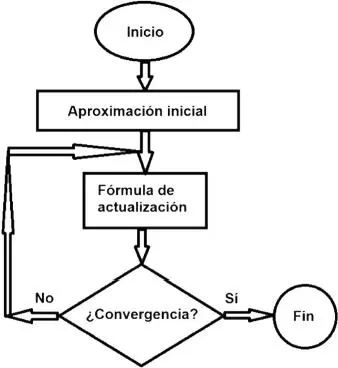
A continuación vamos a presentar los métodos más comunes para resolver ecuaciones no lineales en una variable.

2.1 Método del punto fijo

Este método solo utiliza el último valor estimado para obtener la siguiente aproximación a la solución. Por esto se denomina a veces iteración funcional. Consideremos la solución de la ecuación escalar:

Ahora calculamos una secuencia {x (k)}; k = 1, 2,..., que si es exitosa, converge a la solución x*. El usuario debe proveer la primera estimación x (1), lo cual no es un paso trivial. Las siguientes aproximaciones están dadas por:

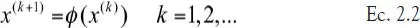
Donde x = φ(x) posee la misma solución que f(x) = 0, es decir, x* = φ(x*).

La fórmula de iteración (o de actualización) x = φ(x) se obtiene por reordenamiento de términos o adición de términos a ambos lados de la ecuación original f(x) = 0. Este proceso de pasar de f(x) = 0 a x = φ(x) no es único, como se ve en el siguiente ejemplo.

Ejemplo 2.1. Método del punto fijo

Considere la ecuación: f(x) = x 3- 7x - 6 = 0. Algunas funciones de iteración posibles son:

φ 1(x) = (x 3- 6)/7

φ 2(x) = (7x + 6)/x 2

φ 3(x) = (2x 3+ 6) /(3x 2- 7)

Como sabemos a priori que f(x) = (x+1)·(x+2)·(x-3), lo que hacemos es probar el desempeño de las fórmulas arriba detalladas cuando escogemos como valor inicial x (1)= -1.1 y x (1)= -2.2, respectivamente.

Haciendo los cálculos con las distintas funciones de iteración, para un error relativo máximo de 10 -5en la solución se obtiene la siguiente tabla de resultados:

TABLA 2.1. Comparación de resultados x*(iteraciones) para distintas funciones de actualización

A continuación se presenta el código Matlab ®utilizado para generar las iteraciones de punto fijo.

function [raíz,err,nit]=punto_fijo(fun,x1,tol,maxit)

% función que ejecuta la iteración de punto fijo (o iteración funcional)

% variables de entrada:

% fun: nombre de la función de actualización

% x1: estimador inicial de la solución (o raíz)

% tol: tolerancia en el error relativo de la raíz; defecto: tol = 1e-5

% maxit: máximo número de iteraciones permitidas; defecto: maxit = 100

% variables de salida:

% raíz: solución de la ecuación original

% err: error relativo estimado para la raíz

% nit: número de iteraciones funcionales realizadas

if nargin<4,

maxit=100;

end

if nargin<3,

tol=1e-5;

end

if nargin<2,

error(‘no se puede calcular nada’);

end

xr=x1;

iter=1;

while (1)

xrold=xr;

xr=fun(xrold);

if xr~=0,

ea=abs((xrold-xr)/xr);

end

iter=iter+1;

if eamaxit,

break;

end

end

raíz=xr;

err=ea;

nit=iter;

Definición:Una función φ: R → R es contracción en un conjunto D ∈ R si existe una constante 0 < L < 1 tal que:

Gráficamente, esto significa que un intervalo dado del dominio D se transforma, mediante la aplicación de φ, en un subconjunto de D. Veamos esto en el siguiente ejemplo.