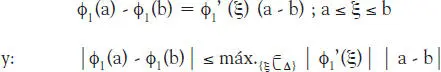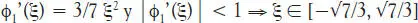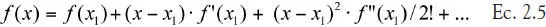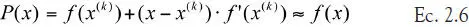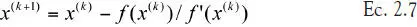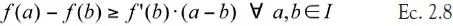Héctor Jorquera González - Métodos numéricos aplicados a Ingeniería

Ejemplo 2.2. Convergencia del método del punto fijo

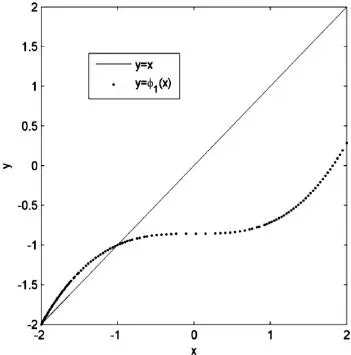
Volvamos a considerar φ 1(x) = (x 3-6)/7 en torno al origen x = 0. Gráficamente, empleando la función fplot , podemos apreciar que el intervalo [0,2] se transforma en el intervalo [-6/7, 2/7], el que claramente no es subconjunto de [0,2], por lo cual φ 1no es una contracción allí. Sin embargo, también es posible apreciar gráficamente que

x ∈ [-2, 0] → φ 1(x) ∈ [-2, -6/7], ∴ φ 1(x) es contracción en D ≡ [-2, 0]

FIGURA 2.2. Función de actualización φ 1(x) para el ejemplo 2.2

% figura 2.2

f1=@(x) x;

f2=@(x) (x^3-6)/7;

fplot(f1,[-2 2],’-k’);

ylim([-2 2]);

axis equal;

hold on

fplot(f2,[-2 2],’k.’);

xlabel(‘x’);

ylabel(‘y’);

legend(‘y=x’,’y=\phi_1(x)’);

Hay que hacer notar que el concepto de contracción está íntimamente asociado al dominio de la función φ 1, y este dominio se supone que contiene la solución buscada de antemano, por lo que nuestra intuición física nos puede dar alguna estimación de cuál debería ser este intervalo, de manera de poder aplicar la definición.

A continuación estableceremos el resultado matemático fundamental en que se basa este método iterativo.

2.2 Teorema de la función contractante (o del punto fijo)

Sea φ una función continua φ: R → R y sea D ∈ R tal que: x∈ D → φ (x) ∈ D. Supongamos además que existe una constante L (0 < L < 1)

tal que

Luego, para todo x (1)∈ D, la secuencia 2.2 converge a un único punto fijo x* ∈ D.

Gráficamente, la secuencia de iteraciones 2.2 hace que la distancia entre un estimador x (k)y la solución x* sea cada vez más pequeña, hasta que tiende a cero, debido a que la constante de Lipschitz L es menor que 1.0. No obstante, para que haya convergencia, se deben cumplir todas las condiciones del teorema anterior, las que se pueden verificar fácilmente empleando la derivada de φ(x) como se ve en el siguiente ejemplo.

Ejemplo 2.3. Verificación de convergencia del método del punto fijo

Consideremos f(x) = x 3- 7x - 6 = 0 y φ 1(x) = (x 3- 6)/7 para hallar la raíz x* = -1

a) Por el ejemplo previo, sabemos que φ 1es una contracción en D = [-2,0] y x* ∈ D.

b) A través del teorema del valor medio se tiene:

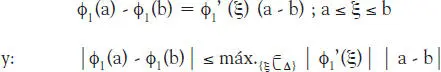
Por lo que tenemos que L ≡ máx. {ξ ∈ Δ}| φ 1’(ξ) |

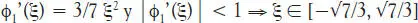
La condición de contracción se cumple si consideramos la intersección de ambos intervalos, luego la región de convergencia es: [-√7/3, 0]; como esta región contiene x* = -1, la iteración de punto fijo con φ 1(x) convergerá a x* = -1, para cualquier valor inicial x (1)∈ [-√7/3, 0].

Verificar esto utilizando la función punto_fijo presentada en el ejemplo 2.1. Adviértase que φ 1(x) no es capaz de calcular la raíz x* = -2. ¿Por qué?

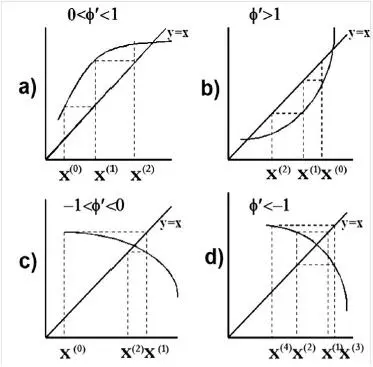
2.2.1 Representación gráfica de la iteración de punto fijo

Para el caso de una ecuación escalar, el comportamiento de la iteración x (k+1)= φ(x (k)) se puede representar como una trayectoria que une los gráficos de y = φ(x) e y = x, como se aprecia en la siguiente figura. Es posible notar que la magnitud y signo de la derivada φ’(x) determinan el éxito o fracaso de la iteración de punto fijo.

FIGURA 2.3. Resultados posibles para una iteración de punto fijo

2.3 Métodos de interpolación

La idea consiste en que la función f(x) = 0 se puede expandir en torno a x = x 1mediante serie de Taylor; se trunca la serie y a esta aproximación a f(x) se le busca(n) el(los) cero(s).

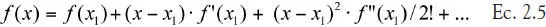
2.3.1 Interpolación lineal (método de Newton)

Expandimos f(x) en torno a x = x (k); llamando P(x) a la aproximación lineal:

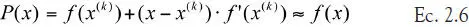
Y la nueva aproximación x (k+1)es la raíz de P(x) = 0:

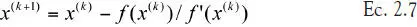
Ejemplo 2.4. Visualización de convergencia del método de Newton

El método de Newton corresponde a una secuencia de interpolaciones lineales, tal como se ilustra en la siguiente figura para el caso de f(x) = x-x 2+0.5x 3, comenzando con x (1)= 3.5.

FIGURA 2.4. Visualización del método de Newton

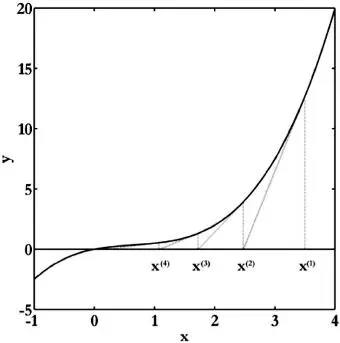
A continuación se presenta el código en Matlab ®empleado para generar la figura anterior, excepto por los títulos x (k)que se añadieron con un editor de imágenes.

% macro para construir la Figura 2.4

f1=@(x) x-x^2+0.5*x^3; % función no lineal f1(x)

f1p=@(x) 1-2*x+1.5*x^2; % derivada de la función f1’(x)

fplot(f1,[-2 4],’k-’);

axis square;

xlabel(‘x’);

ylabel(‘y’);

hold on;

plot([-2 4],[0 0],’k-’)

% secuencia iterativa del método de Newton

x(1)=3.5;

f(1)=f1(x(1));

for i=2:4,

% iteración del método de Newton

x(i)=x(i-1)-f(i-1)/f1p(x(i-1));

f(i)=f1(x(i));

% secuencia de gráficos del método de Newton

xpl=[x(i-1) x(i-1)];

fpl=[0 f(i-1)];

plot(xpl,fpl,’k:’);

xpl=[x(i-1) x(i)];

fpl=[f(i-1) 0];

plot(xpl,fpl,’k:’);

end

Notas:

i) La función de actualización es: φ(x) = x - f(x)/f’(x)

ii) El método es de segundo orden: cuadráticamente convergente. Esto significa que el número de cifras decimales correctas se duplica en cada iteración cuando x (k)→ x*

Podemos apreciar en la ecuación 2.7 que define la actualización del método de Newton, que se pueden presentar problemas si cerca de la solución buscada la derivada f’ se hace cero o muy pequeña. El siguiente teorema nos aclara qué se puede esperar de la iteración 2.7.

Teorema:Si la solución x* de f(x) = 0 está en un intervalo I en donde f’(x) ≠ 0 y además f’ es continua en I y se cumple la condición de convexidad:

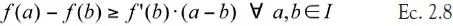
Entonces para todo x (0)∈ I, la iteración de Newton produce una secuencia {x (k)} que satisface exactamente una de las siguientes condiciones:

i) x (k)∈ I y la secuencia {x (k)} converge monótonamente a x*