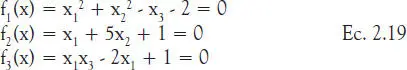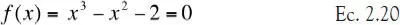Héctor Jorquera González - Métodos numéricos aplicados a Ingeniería

a) Podemos remplazar J (k)por una matriz Aconstante, con lo que se obtiene el método de la cuerda paralela:

b) Si escogemos A = I, tenemos una iteración de punto fijo en cada variable por separado, con pérdida de rapidez de convergencia. Una elección más apropiada es A = J (0), con lo cual la iteración queda:

Esta se utiliza frecuentemente en resolución de ecuaciones diferenciales ordinarias por métodos implícitos (capítulo 3). Generalmente, el jacobiano Jse revalúa cada m iteraciones, para mejorar la rapidez de convergencia.

c) Cuando las derivadas parciales no se entregan explícitamente, el jacobiano se puede determinar por diferencias finitas. Esto conduce al método de Newton discreto:

Comentarios:

De las aproximaciones recién comentadas se desprenden dos desventajas:

i) Hay que evaluar el jacobiano (a veces por diferencias finitas). Esto implica n 2operaciones por paso (se puede reducir si se actualiza el jacobiano cada m iteraciones).

ii) La solución para d (k)implica n 3/3 operaciones por iteración, aunque si el jacobiano se fija, esto significa n 2operaciones/iteración.

En general, las funciones fson caras de evaluar en problemas de ingeniería de procesos, por lo que los métodos de Newton son costosos en términos de tiempo computacional. Para disminuir el número de operaciones/iteración, se recurre a los métodos de cuasi-Newton, que usan una aproximación al jacobiano, los que son actualizados en cada paso a fin de reducir el número de operaciones. Para más detalles acerca de estos métodos, se recomienda consultar el artículo de Sargent [2] y el de Dennis y Mori [3].

El siguiente ejemplo muestra un código Matlab ®para resolver un sistema de n ecuaciones usando el método de Newton discreto 2.18. Se calcula cada columna ‘j’ del jacobiano introduciendo una perturbación a la variable ‘j’ mediante diferencias finitas.

Ejemplo 2.6. Aplicación del método de Newton discreto en N variables

Se desea resolver el sistema de ecuaciones no lineales:

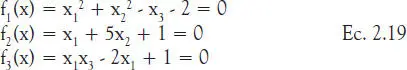
Se usa el método de Newton discreto. El método programado debe controlar que el número de iteraciones no exceda un valor máximo, y como criterio de error utilizar la norma del vector f: err = || f( x (k))||= norm ( f) que debe ser menor a 1·10 -5. ¿Cuántas raíces distintas encuentra usted?

La siguiente tabla muestra los resultados de aplicar el método de Newton discreto al sistema de ecuaciones anterior, con distintos vectores iniciales x (1). En este caso encontramos tres raíces diferentes. Esto se debe a que si eliminamos x 2y x 3en las ecuaciones del sistema, hallamos una ecuación cúbica para x 1, la cual posee tres raíces reales distintas. La función que implementa el método de Newton y el sistema de ecuaciones se entregan a continuación de la tabla; hay que hacer notar que el vector f(x)debe ser un vector columna.

TABLA 2.3. Solución del ejemplo 2.6

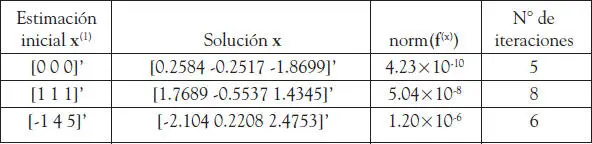
A continuación el listado del macro de Matlab ®que resuelve el ejemplo 2.6.

function [raiz,f,err,nit]=newton_dis_N(fun,x1,tol,maxit)

% Esta rutina resuelve un sistema de ecuaciones no lineales usando el método clásico de

% Newton-Raphson con jacobiano discreto. Variables de entrada:

% fun: función externa que calcula el vector f(x)

% x0: vector inicial estimado para la solución

% tol: tolerancia en error relativo de x

% maxit: máximo número de iteraciones aceptable

% variables de salida:

% raíz: vector solución estimada

% f: valor de la función en la solución estimada

% err: estimación del error alcanzado

% nit: número de iteraciones realizadas por el método

if nargin<4,

maxit=100;

end

if nargin<3,

tol=1e-5;

end

if nargin<2,

error(‘no se puede calcular nada’);

end

%% inicialización del cálculo

xr=x1; iter=0;

ep=1e-4; % incremento para calcular diferencias finitas en el jacobiano

N=length(x1); I=eye(N); J=zeros(N,N);

%% ciclo principal del cálculo

while (1)

xrold=xr;

f=fun(xrold);

for j=1:N,

J(:,j)=(fun(xrold+ep*I(:,j))-f)/ep;

end

xr=xrold-J\f;

ef=norm(f); % error en la norma de f(x)

iter=iter+1; % incremento del número de iteraciones

if efmaxit,

break;

end

end

%% asignación de variables de salida

raiz=xr; err=ef; nit=iter;

function y = f1(x)

%sistema de ecuaciones no lineales del ejemplo 2.5

y(1) = x(1)^2+x(2)^2-x(3)-2;

y(2) = x(1)+5*x(2)+1;

y(3) = x(1)*x(3)-2*x(1)+1;

y = y(:);

2.4.2. Rutinas implementadas en Matlab ®para sistemas de ecuaciones

En el caso de sistemas de ecuaciones lineales, Matlab ®tiene como herramienta básica de resolución la rutina fsolve . Esta rutina recibe como argumentos mínimos una función de Matlab ®donde se expresa el sistema de ecuaciones como función del vector x, que es el segundo argumento mínimo requerido por fsolve . La función puede aplicar tres algoritmos diferentes: Gauss-Newton, Levenberg-Marquardt y Región de Confianza, y por defecto calcula el jacobiano del sistema de ecuaciones por diferencias finitas.

Si esta función tiene dificultades para hallar la solución, sobre todo cuando la dimensión de xaumenta, entonces se puede intentar minimizar la función escalar f(x)· f(x), que es mínima cuando f(x) = 0. Así se puede probar con fminunc que minimiza una función escalar de un vector xsin restricciones, o bien probar fmincon que opera con restricciones y por tanto reduce el espacio de búsqueda de la solución.

2.5 Problemas propuestos

2.5.1 Método del punto fijo para ecuaciones escalares

1) Considere la resolución de la ecuación cúbica:

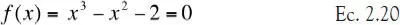
Se propone encontrar una raíz positiva (>1) de la ecuación anterior, utilizando las siguientes funciones de actualización:

a) Despejando la raíz cúbica, llámela φ 1(x) = (x 2+2) 1/3

b) Despejando la raíz cuadrada, llámela φ 2(x) = (x 3-2) 1/2

Realice iteraciones del punto fijo usando las dos funciones de actualización ya descritas. Indique si las iteraciones están convergiendo o no, y por qué se produce tal comportamiento.

2) Para el flujo turbulento en una cañería lisa, el factor de fricción c viene dado por la solución de la ecuación algebraica: