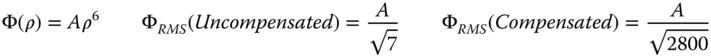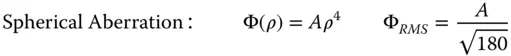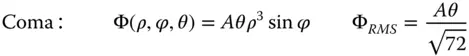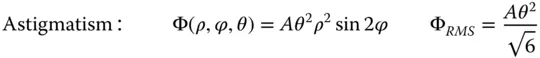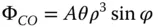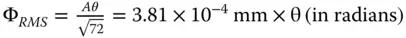Stephen Rolt - Optical Engineering Science

The rms wavefront error has thus been reduced by a factor of six by the focus compensation process. Furthermore, this analysis feeds in to the discussion in Chapter 3on the use of balancing aberrations to minimise wavefront error. For example, if we have succeeded in eliminating third order spherical aberration and are presented with residual fifth order spherical aberration, we can minimise the rms wavefront error by balancing this aberration with a small amount of third order aberration in addition to defocus. Analysis using Zernike polynomials is extremely useful in resolving this problem:

As previously outlined, the uncompensated rms wavefront error may be calculated from the RSS sum of all the four Zernike terms. Naturally, for the compensated system, we need only consider the first term.

(5.24)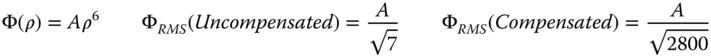

For the fifth order spherical aberration, the rms wavefront error has been reduced by a factor of 20 through the process of aberration balancing. In terms of the practical application of this process, one might wish to optimise an optical design by minimising the rms wavefront error. Although, in practice, the process of optimisation will be carried out using software tools, nonetheless, it is useful to recognise some key features of an optimised design. By virtue of the previous example, optimisation of spherical aberration should lead to an OPD profile that is close to the 5th order Zernike term. This is shown in Figure 5.5which illustrates the profile of an optimised OPD based entirely on the relevant fifth order Zernike term. The graph plots the nominal OPD again the normalised pupil function with the form given by the Zernike polynomial, n = 6, m = 0.

In the optimisation of an optical design it is important to understand the form of the OPD fan displayed in Figure 5.5in order recognise the desired endpoint of the optimisation process. It displays three minima and two maxima (or vice versa), whereas the unoptimised OPD fan has one fewer maximum and minimum. Thus, although the design optimisation process itself might be computer based, nevertheless, understanding and recognising the how the process works and its end goal will be of great practical use. That is to say, as the computer-based optimisation proceeds, on might expect the OPD fan to acquire a greater number of maxima and minima.

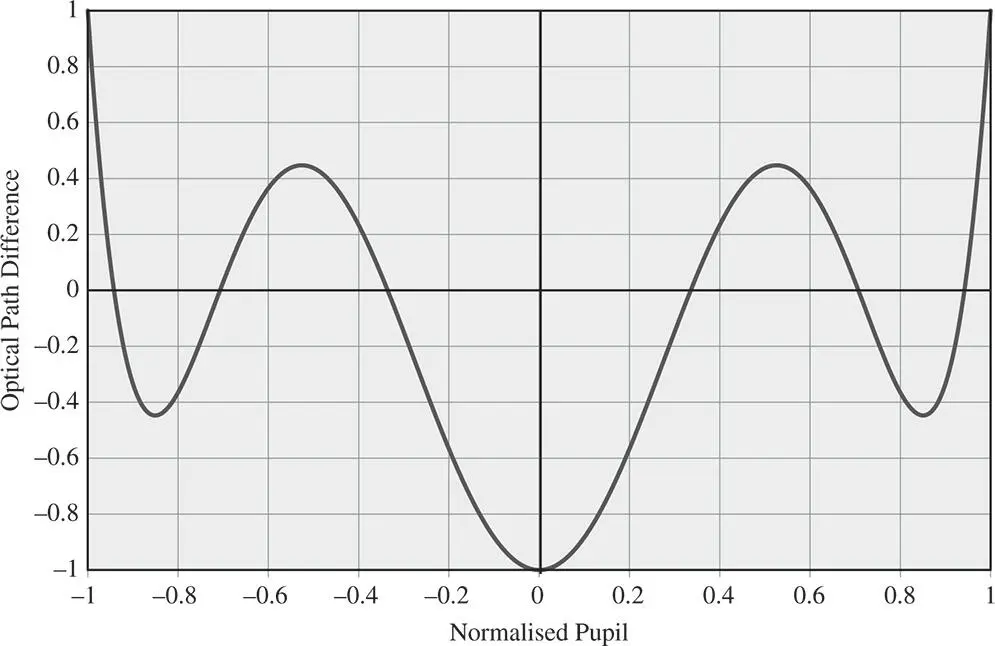
Figure 5.5 Fifth order Zernike polynomial and aberration balancing.

One can apply the same analysis to all the Gauss-Seidel aberrations and calculate its associated rms wavefront error.

(5.25a)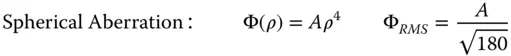

(5.25b)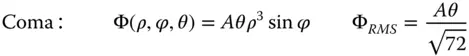

(5.25c)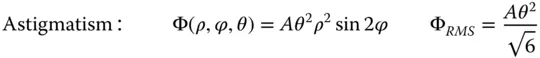

(5.25d)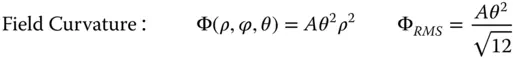

θ represents the field angle

Equations (5.25a)– (5.25d)are of great significance in the analysis of image quality, as the rms wavefront error is a key parameter in the description of the optical quality of a system. This will be discussed in more detail in the next chapter.

Worked Example 5.2A plano-convex lens, with a focal length of 100 mm is used to focus a collimated beam; the refractive index of the lens material is 1.52. It is assumed that the curved surface faces the infinite conjugate. The pupil diameter is 12.5 mm and the aperture is situated at the lens. What is the rms spherical aberration produced by this lens – (i) at the paraxial focus; (ii) at the compensated focus? What is the rms coma for a similar collimated beam with a field angle of one degree?

Firstly, we calculate the spherical aberration of the single lens. With the object at infinity and the image at the first focal point, the conjugate parameter, t , is equal to −1. The shape parameter, s , for the plano convex lens is equal to 1 since the curved surface is facing the object. From Eq. (4.30a)the spherical aberration of the lens is given by:

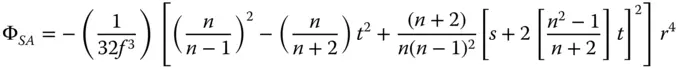
r max= 6.25 mm (12.5/2); f = 100 mm; n = 1.52; s = 1; t = −1

By substituting these values into the above equation, the spherical aberration may be directly calculated:

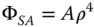
where A = 4.13 × 10 −4mm ρ = r / r max

From Eq. (5.23), the uncompensated rms wavefront error is A/√5 and the compensated error is A/√180. Therefore the rms values are given by:

Φ rms (paraxial) = 185 nm; Φ rms (compensated) = 30.8 nm

Secondly, we calculate the coma. From (4.30b), the coma of the lens is given by:

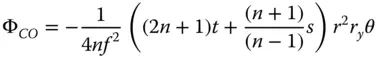
Again, substituting the relevant values for f , n , r max, s , and t , we get:

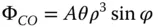
where A = 3.24 × 10 −3mm ρ = r / r max r y= r sin ϕ

From (5.25b)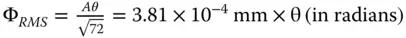

We are told that θ = 1° or 0.0174 rad. Therefore, Φ rms = 6.66 × 10 −6 or 6.66 nm

We have emphasised the synergy between Zernike polynomials and the classical treatment of aberrations in an axially symmetric optical system, i.e. the Gauss-Seidel aberrations. However, in practice, in real optical systems, these axial symmetries are often compromised, either by accident or by design. Some systems are deliberately designed whereby not all optical surfaces are aligned to a common axis. These will inevitably introduce non-standard wavefront aberrations into the system. Most significantly, even with a symmetrical design, component manufacturing errors and system alignment may introduce more complex wavefront errors into the system. Naturally, alignment errors create an off-axis optical system ‘by accident’. Manufacturing or polishing errors might produce an optical surface whose shape departs from that of an ideal sphere or conic in a somewhat complex fashion. For example, the effects of these errors may be to introduce a trefoil term ( n = 3, m = 3) into the wavefront error; this is not a standard Gauss-Seidel term.