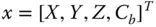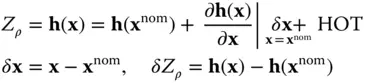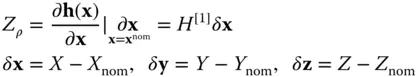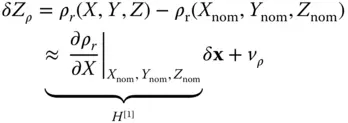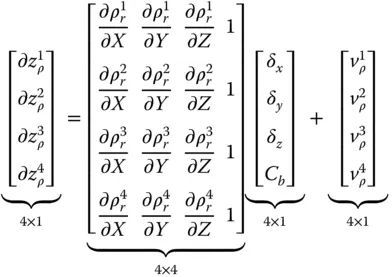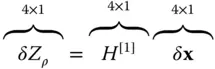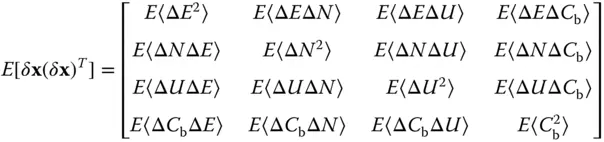Mohinder S. Grewal - Global Navigation Satellite Systems, Inertial Navigation, and Integration
Здесь есть возможность читать онлайн «Mohinder S. Grewal - Global Navigation Satellite Systems, Inertial Navigation, and Integration» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Global Navigation Satellite Systems, Inertial Navigation, and Integration
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:4 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Global Navigation Satellite Systems, Inertial Navigation, and Integration: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Global Navigation Satellite Systems, Inertial Navigation, and Integration»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
GNSSs including GPS, Glonass, Galileo, BeiDou, QZSS, and IRNSS/NAViC,
and MATLAB programs on square root information filtering (SRIF)
This book provides readers with solutions to real-world problems associated with global navigation satellite systems, inertial navigation, and integration. It presents readers with numerous detailed examples and practice problems, including GNSS-aided INS, modeling of gyros and accelerometers, and SBAS and GBAS. This revised fourth edition adds new material on GPS III and RAIM. It also provides updated information on low cost sensors such as MEMS, as well as GLONASS, Galileo, BeiDou, QZSS, and IRNSS/NAViC, and QZSS. Revisions also include added material on the more numerically stable square-root information filter (SRIF) with MATLAB programs and examples from GNSS system state filters such as ensemble time filter with square-root covariance filter (SRCF) of Bierman and Thornton and SigmaRho filter.
Global Navigation Satellite Systems, Inertial Navigation, and Integration, 4th Edition Updates on the significant upgrades in existing GNSS systems, and on other systems currently under advanced development Expanded coverage of basic principles of antenna design, and practical antenna design solutions More information on basic principles of receiver design, and an update of the foundations for code and carrier acquisition and tracking within a GNSS receiver Examples demonstrating independence of Kalman filtering from probability density functions of error sources beyond their means and covariances New coverage of inertial navigation to cover recent technology developments and the mathematical models and methods used in its implementation Wider coverage of GNSS/INS integration, including derivation of a unified GNSS/INS integration model, its MATLAB implementations, and performance evaluation under simulated dynamic conditions
is intended for people who need a working knowledge of Global Navigation Satellite Systems (GNSS), Inertial Navigation Systems (INS), and the Kalman filtering models and methods used in their integration.


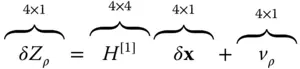
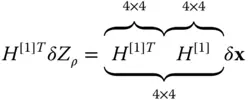
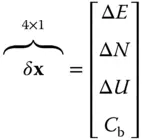
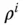 is the pseudorange to the i th satellite and C bis the residual satellite clock bias and receiver clock bias, where an estimate of the satellite clock error from the GNSS ground control segment has been removed from C b.
is the pseudorange to the i th satellite and C bis the residual satellite clock bias and receiver clock bias, where an estimate of the satellite clock error from the GNSS ground control segment has been removed from C b.