Mark W. Spong - Robot Modeling and Control

(2.51)

Note, since k is a unit vector, that the length of the vector r is the equivalent angle θ and the direction of r is the equivalent axis k .

One should be careful to note that the representation in Equation ( 2.51) does not mean that two axis-angle representations may be combined using standard rules of vector algebra, as doing so would imply that rotations commute which, as we have seen, is not true in general.

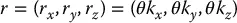
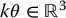In this section we introduce the so-called exponential coordinatesand give an alternate description of the axis-angle transformation ( 2.44). We showed above in Section 2.5.3 that any rotation matrix R ∈ SO (3) can be expressed as an axis-angle matrix R k, θusing Equation ( 2.44). The components of the vector are called exponential coordinatesof R .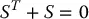

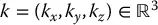To see why this terminology is used, we first recall from Appendix B the definition of so (3) as the set of 3 × 3 skew-symmetricmatrices S satisfying

(2.52)

For let S ( k ) be the skew-symmetric matrix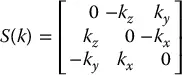

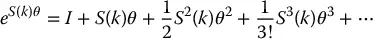
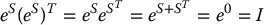
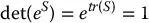
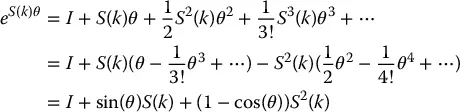
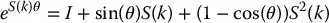
(2.53)

and let e S(k)θbe the matrix exponential as defined in Appendix B

(2.54)

Then we have the following proposition, which gives an important relationship between SO (3) and so (3).

Proposition 2.1

The matrix e S(k)θis an element of SO (3) for any S ( k ) ∈ so (3) and, conversely, every element of SO (3) can be expressed as the exponential of an element of so (3).

Proof:To show that the matrix e S(k)θis in SO (3) we need to show that e S(k)θis an orthogonal matrix with determinant equal to + 1. To show this we rely on the following properties that hold for any n × n matrices A and B

1

2 If the n × n matrices A and B commute, i.e., AB = BA, then eAeB = e(A + B)

3 The determinant , where tr(A) is the trace of A.

The first two properties above can be shown by direct calculation using the series expansion ( 2.54) for eA . The third property follows from the Jacobi Identity(Appendix B). Now, since ST = − S , if S is skew-symmetric, then S and ST clearly commute. Therefore, with S = S ( k θ ) ∈ so (3), we have

(2.55)

which shows that e S(kθ)is an orthogonal matrix. Also

(2.56)

since the trace of a skew-symmetric matrix is zero. Thus e S(kθ)∈ SO (3) for S ( k θ ) ∈ so (3).

The converse, namely, that every element of SO (3) is the exponential of an element of so (3), follows from the axis-angle representation of R and Rodrigues’ formula, which we derive next.

Given the skew-symmetric matrix S ( k ) it is easy to show that S 3( k ) = − S ( k ), from which it follows that S 4( k ) = − S 2( k ), etc. Thus the series expansion for e S(k)θreduces to

the latter equality following from the series expansion of the sine and cosine functions. The expression

(2.57)

is known as Rodrigues’ formula. It can be shown by direct calculation that the angle-axis representation for R k, θgiven by Equation ( 2.44) and Rodrigues’ formula in Equation ( 2.57) are identical.

Remark 2.1.

The above results show that the matrix exponential function defines a one-to-one mapping from so(3) onto SO(3). Mathematically, so(3) is a Lie algebra and SO (3) is a Lie group.

We have now seen how to represent both positions and orientations. We combine these two concepts in this section to define a rigid motionand, in the next section, we derive an efficient matrix representation for rigid motions using the notion of homogeneous transformation.

Definition 2.2.

A rigid motion is an ordered pair ( d , R ) where and R ∈ SO (3). The group of all rigid motions is known as the special Euclidean group and is denoted by SE (3). We see then that .

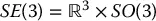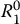A rigid motion is a pure translation together with a pure rotation. 3Let be the rotation matrix that specifies the orientation of frame o 1 x 1 y 1 z 1with respect to o 0 x 0 y 0 z 0, and 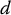be the vector from the origin of frame o 0 x 0 y 0 z 0to the origin of frame o 1 x 1 y 1 z 1. Suppose the point 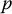is rigidly attached to coordinate frame o 1 x 1 y 1 z 1, with local coordinates 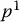. We can express the coordinates of 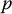with respect to frame o 0 x 0 y 0 z 0using