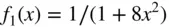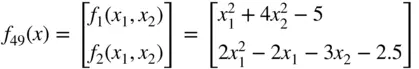Won Y. Yang - Applied Numerical Methods Using MATLAB

MATLAB has several three‐dimensional (3D) graphic plotting commands such as ‘ plot3()’, ‘ mesh()’, and ‘ contour()’. ‘ plot3()’ plots a two‐dimensional (2D) valued‐function of a scalar‐valued variable; ‘ mesh()’/‘ contour()’ plots a scalar valued‐function of a 2D variable in a mesh/contour‐like style, respectively.

Readers are recommended to use the ‘ help’ command for detailed usage of each command. Try running the above MATLAB script “nm01f04.m” to see what figures will appear ( Figure 1.4).

%nm01f04.m: to plot 3D graphs t=0:pi/50:6*pi; expt= exp(-0.1*t); xt= expt.*cos(t); yt= expt.*sin(t); % dividing the screen into 2x2 sections clf subplot(521), plot3(xt,yt,t), grid on %helix subplot(522), plot3(xt,yt,t), grid on, view([0 0 1]) subplot(523), plot3(t,xt,yt), grid on, view([1 -3 1]) subplot(524), plot3(t,yt,xt), grid on, view([0 -3 0]) x=-2:.1:2; y=-2:.1:2; [X,Y] = meshgrid(x,y); Z =X.̂2 + Y.̂2; subplot(525), mesh(X,Y,Z), grid on %[azimuth,elevation]=[-37.5,30] subplot(526), mesh(X,Y,Z), view([0,20]), grid on pause, view([30,30]) subplot(527), contour(X,Y,Z) subplot(528), contour(X,Y,Z,[.5,2,4.5])

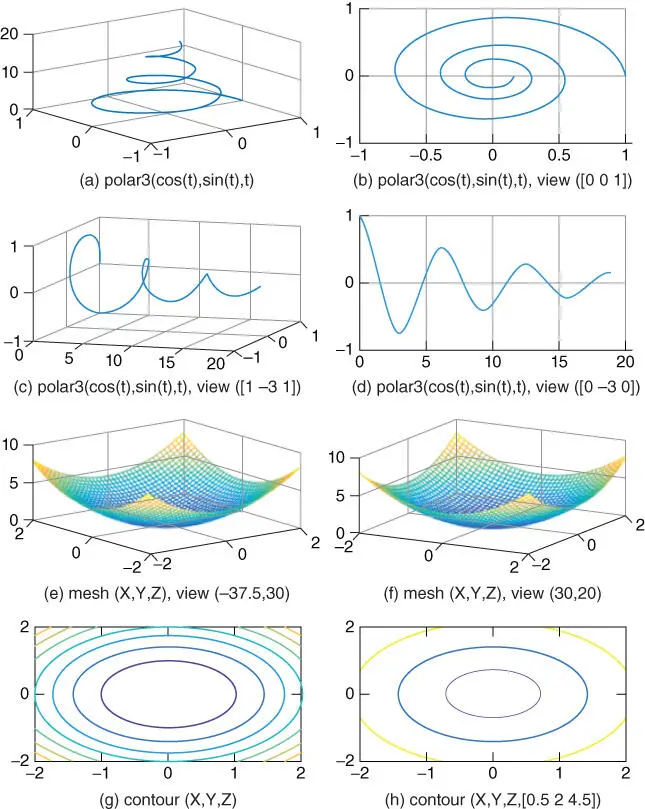
Figure 1.43D graphs drawn by using plot3(), mesh(), and contour().

Mathematical functions and special reserved constants/variables defined in MATLAB are listed in Table 1.3.

Table 1.3Functions and variables inside MATLAB.

Function	Remark	Function	Remark
cos(x)		exp(x)	Exponential function
sin(x)		log(x)|	Natural logarithm
tan(x)		log10(x)	Common logarithm
acos(x)	cos −1( x )	abs(x)	Absolute value
asin(x)	sin −1( x )	angle(x)	Phase of a complex number (rad)
atan(x)	‐ π /2 ≤ tan −1( x ) ≤ π /2	sqrt(x)	Square root
atan2(y,x)	‐ π ≤ tan −1( y / x ) ≤ π	real(x)	Real part
cosh(x)	( e x+ e −x)/2	imag(x)	Imaginary part
sinh(x)	( e x− e −x)/2	conj(x)	Complex conjugate
tanh(x)	( e x− e −x)/( e x+ e −x)	round(x)	The nearest integer (round‐off)
acosh(x)	cosh −1( x )	fix(x)	The nearest integer toward 0
asinh(x)	sinh −1( x )	floor(x)	The greatest integer ≤ x
atanh(x)	tanh −1( x )	ceil(x)	The smallest integer ≥ x
max	Maximum and its index	sign(x)	1 (positive)/0/−1 (negative)
min	Minimum and its index	mod(y,x)	Remainder of y / x
sum	Sum	rem(y,x)	Remainder of y / x
prod	Product	eval(f)	Evaluate an expression
norm	Norm	feval(f,a)	Function evaluation
sort	Sort in the ascending order	polyval	Value of a polynomial function
clock	Present time	poly	Polynomial with given roots
find	Index of element(s) satisfying given condition	roots	Roots of polynomial
flops(0)	Reset the flops count to zero	tic	Start a stopwatch timer
flops	Cumulative # of floating point op eration s (no longer available)	toc	Read the stopwatch timer (elapsed time from tic)
date	Present date	magic	Magic square
	Reserved variables with special meaning
i, j		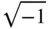pi	π
eps	Machine epsilon	Inf, inf	Largest number (∞)
realmax, realmin	Largest/smallest positive number	NaN	Not_a_Number (undetermined)
end	The end of for‐loop or if, while, case statement or an array index	break	Exit while/for loop
nargin	# of input arguments	nargout	# of output arguments
varargin	Variable input argument list	varargout	Variable output argument list

MATLAB also allows us to define our own function and store it in a file named after the function name so that it can be used as if it were a built‐in function. For instance, we can define a scalar‐valued function:

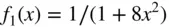
and a vector‐valued function

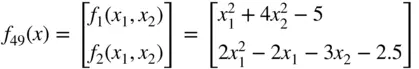
as follows:

Once we store these functions as M‐files, each named “f1.m” and “f49.m” after the function names, respectively, we can call and use them as needed inside another M‐file or in the MATLAB Command window.

>f1([0 1]) % several values of a scalar function of a scalar variable ans= 1.0000 0.1111 >f49([0 1]) % a value of a 2D vector function of a vector variable ans= -1.0000 -5.5000 >feval('f1',[0 1]), feval('f49',[0 1]) % equivalently, yields the same ans= 1.0000 0.1111 ans= -1.0000 -5.5000

1 (Q7) With the function f1(x) defined as a scalar function of a scalar variable, we enter a vector as its input argument to obtain a seemingly vector‐valued output. What's going on?

2 (A7) It is just a set of function values [f1(x1) f1(x2) …] obtained at a time for several values [x1 x2 …] of x. In expectation of one‐shot multioperation, it is a good practice to put a dot ( .) just before the arithmetic operators *(multiplication), /(division), and ̂(power) in the function definition so that the element‐by‐element (element‐wise or term‐wise) operation can be done any time.