The results of various operations on these vectors/matrices are as follows (pay attention to the error message):
>A3=A1+A2, A4=A1-A2, 1+A1 % matrix/scalar addition/subtraction A3= -2 4 6 A4= 0 0 0 ans= 0 3 4 2 5 3 6 5 1 5 6 3 >AB=A1*B % 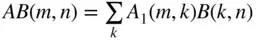 matrix multiplication? Error using * Inner matrix dimensions must agree. >BA1=B*A1 % regular matrix multiplication BA1=-9 -8 -1 3 -6 -9 >AA=A1.*A2 % element-wise (term-wise) multiplication AA= 1 4 9 -8 0 2 >AB=A1.*B %AB(m, n) = A1(m, n)B(m, n) element-wise multiplication Error using .* Matrix dimensions must agree. >A1_1=pinv(A1),A1'*(A1*A1')̂-1,eye(size(A1,2))/A1 %
matrix multiplication? Error using * Inner matrix dimensions must agree. >BA1=B*A1 % regular matrix multiplication BA1=-9 -8 -1 3 -6 -9 >AA=A1.*A2 % element-wise (term-wise) multiplication AA= 1 4 9 -8 0 2 >AB=A1.*B %AB(m, n) = A1(m, n)B(m, n) element-wise multiplication Error using .* Matrix dimensions must agree. >A1_1=pinv(A1),A1'*(A1*A1')̂-1,eye(size(A1,2))/A1 % 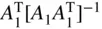 A1_1= -0.1914 0.1399 %right inverse of a 2x3 matrix A1 0.0617 0.0947 0.2284 -0.0165 >A1*A1_1 %A1/A1=I implies the validity of A5_1 as the right inverse ans= 1.0000 0.0000 0.0000 1.0000 >A5=A1'; % a 3x2 matrix >A5_1=pinv(A5),(A5'*A5)̂-1*A5',A5\eye(size(A5,1)) %
A1_1= -0.1914 0.1399 %right inverse of a 2x3 matrix A1 0.0617 0.0947 0.2284 -0.0165 >A1*A1_1 %A1/A1=I implies the validity of A5_1 as the right inverse ans= 1.0000 0.0000 0.0000 1.0000 >A5=A1'; % a 3x2 matrix >A5_1=pinv(A5),(A5'*A5)̂-1*A5',A5\eye(size(A5,1)) % 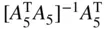 A5_1= -0.1914 0.0617 0.2284 %left inverse of a 3x2 matrix A5 0.1399 0.0947 -0.0165 >A5_1*A5 %A5\A5=I implies the validity of A5_1 as the left inverse ans= 1.0000 -0.0000 -0.0000 1.0000 >A1_li=(A1'*A1)̂-1*A1' %the left inverse of matrix A1 with M
A5_1= -0.1914 0.0617 0.2284 %left inverse of a 3x2 matrix A5 0.1399 0.0947 -0.0165 >A5_1*A5 %A5\A5=I implies the validity of A5_1 as the left inverse ans= 1.0000 -0.0000 -0.0000 1.0000 >A1_li=(A1'*A1)̂-1*A1' %the left inverse of matrix A1 with M
1 (Q14) Does the left inverse of a matrix having rows fewer than columns exist?
2 (A14) No. There is no N × M matrix that is premultiplied on the left of an M × N matrix with M < N to yield a nonsingular matrix, far from an identity matrix. In this context, MATLAB should have rejected the above case on the ground that is singular and so its inverse does not exist. But, because the round‐off errors make a very small number appear to be a zero or a real zero appear to be a very small number (as will be mentioned in Remark 2.3), it is not easy for MATLAB to tell a near‐singularity from a real singularity. That is why MATLAB dares not to declare the singularity case and instead issues just a warning message to remind you to check the validity of the result so that it will not be blamed for a delusion. Therefore, you must be alert for the condition mentioned in Remark 1.1(2), which says that, in order for the left inverse to exist, the number of rows must not be less than the number of columns.>A1_li*A1 %No identity matrix, since A1_li isn't the left inverse ans = 1.2500 0.7500 -0.2500 -0.2500 0.5000 0.7500 1.5000 3.5000 2.5000 >det(A1'*A1) %A1 is not left-invertible for A1'*A1 is singular ans = 0
3 (cf) Let us be nice to MATLAB as it is to us. From the standpoint of promoting mutual understanding between us and MATLAB, we acknowledge that MATLAB tries to show us apparently good results to please us like always, sometimes even pretending not to be obsessed by the demon of ‘ill‐condition’ in order not to make us feel uneasy. How kind MATLAB is! But, we should be always careful not to be spoiled by its benevolence and not to accept the computing results every inch as it is. In this case, even though the matrix [A1'*A1] is singular and so not invertible, MATLAB tried to invert it and that's all. MATLAB must have felt something abnormal as can be seen from the ominous warning message prior to the computing result. Who would blame MATLAB for being so thoughtful and loyal to us? We might well be rather touched by its sincerity and smartness.
In the aformentioned statements, we see the slash( /)/backslash( \) operators. These operators are used for right/left division, respectively; B/Ais the same as B*inv(A)and A\Bis the same as inv(A)*Bwhen Ais invertible and the dimensions of Aand Bare compatible. Noting that B/Ais equivalent to (A'\B')', let us take a close look at the function of the backslash( \) operator.
>X=A1\A1 % an identity matrix? X= 1.0000 0 -0.8462 0 1.0000 1.0769 0 0 0
1 (Q13) It seems that A1\A1 should have been an identity matrix, but it is not, contrary to our expectation. Why?
2 (A13) We should know more about the various functions of the backslash( \), which can be seen by typing ‘ help slash’ into the MATLAB Command window. Let Remark 1.2 answer this question in cooperation with the next case.>A1*X-A1 %zero if X is the solution to A1*X=A1? ans= 1.0e-015 * 0 0 0 0 0 -0.4441
Remark 1.2The Function of Backslash( \) Operator
Overall, for the command ‘ A\B’, MATLAB finds a solution to the equation A*X=B. Let us denote the row/column dimension of the matrix Aby Mand N.
1 (1) If matrix A is square and upper/lower‐triangular in the sense that all of its elements below/above the diagonal are zero, then MATLAB finds the solution by applying backward/ forward substitution method (Section 2.2.1).
2 (2) If matrix A is square, symmetric (Hermitian), and positive definite, then MATLAB finds the solution by using Cholesky factorization (Section 2.4.2).
3 (3) If matrix A is square and has no special feature, then MATLAB finds the solution by using lower‐upper (LU) decomposition (Section 2.4.1).
4 (4) If matrix A is rectangular, then MATLAB finds a solution by using QR factorization (Section 2.4.2). In case A is rectangular and of full rank with rank( A) = min( M, N), it will be the least‐squares (LSs) solution (Eq. (2.1.10)) for M> N (over‐determined case) and one of the many solutions that is not always the same as the minimum‐norm solution (Eq. (2.1.7)) for M< N (under‐determined case). But for the case where A is rectangular and has rank deficiency, what MATLAB gives us may be useless. Therefore, you must pay attention to the warning message about rank deficiency, which might tell you not to count on the dead‐end solution made by the backslash(\) operator. To find an alternative in the case of rank deficiency, you had better resort to the singular value decomposition (SVD) (see Problem 2.8 for details).
For the moment, let us continue to try more operations on matrices.
>A1./A2 % termwise right division ans= 1 1 1 -2 Inf 2 >A1.\A2 % termwise left division ans= 1 1 1 -0.5 0 0.5 >format rat, B̂-1 %represent the numbers (of B‐1

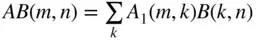 matrix multiplication? Error using * Inner matrix dimensions must agree. >BA1=B*A1 % regular matrix multiplication BA1=-9 -8 -1 3 -6 -9 >AA=A1.*A2 % element-wise (term-wise) multiplication AA= 1 4 9 -8 0 2 >AB=A1.*B %AB(m, n) = A1(m, n)B(m, n) element-wise multiplication Error using .* Matrix dimensions must agree. >A1_1=pinv(A1),A1'*(A1*A1')̂-1,eye(size(A1,2))/A1 %
matrix multiplication? Error using * Inner matrix dimensions must agree. >BA1=B*A1 % regular matrix multiplication BA1=-9 -8 -1 3 -6 -9 >AA=A1.*A2 % element-wise (term-wise) multiplication AA= 1 4 9 -8 0 2 >AB=A1.*B %AB(m, n) = A1(m, n)B(m, n) element-wise multiplication Error using .* Matrix dimensions must agree. >A1_1=pinv(A1),A1'*(A1*A1')̂-1,eye(size(A1,2))/A1 % 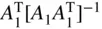 A1_1= -0.1914 0.1399 %right inverse of a 2x3 matrix A1 0.0617 0.0947 0.2284 -0.0165 >A1*A1_1 %A1/A1=I implies the validity of A5_1 as the right inverse ans= 1.0000 0.0000 0.0000 1.0000 >A5=A1'; % a 3x2 matrix >A5_1=pinv(A5),(A5'*A5)̂-1*A5',A5\eye(size(A5,1)) %
A1_1= -0.1914 0.1399 %right inverse of a 2x3 matrix A1 0.0617 0.0947 0.2284 -0.0165 >A1*A1_1 %A1/A1=I implies the validity of A5_1 as the right inverse ans= 1.0000 0.0000 0.0000 1.0000 >A5=A1'; % a 3x2 matrix >A5_1=pinv(A5),(A5'*A5)̂-1*A5',A5\eye(size(A5,1)) % 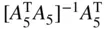 A5_1= -0.1914 0.0617 0.2284 %left inverse of a 3x2 matrix A5 0.1399 0.0947 -0.0165 >A5_1*A5 %A5\A5=I implies the validity of A5_1 as the left inverse ans= 1.0000 -0.0000 -0.0000 1.0000 >A1_li=(A1'*A1)̂-1*A1' %the left inverse of matrix A1 with M
A5_1= -0.1914 0.0617 0.2284 %left inverse of a 3x2 matrix A5 0.1399 0.0947 -0.0165 >A5_1*A5 %A5\A5=I implies the validity of A5_1 as the left inverse ans= 1.0000 -0.0000 -0.0000 1.0000 >A1_li=(A1'*A1)̂-1*A1' %the left inverse of matrix A1 with M










