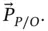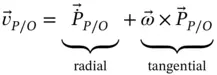We now simply add the relative acceleration vectors to arrive at the absolute acceleration of point  . That is,
. That is,
(1.36) 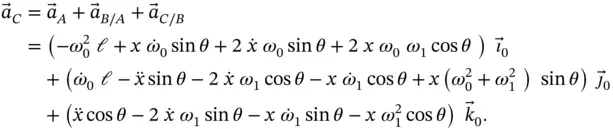
1.6 Absolute Angular Velocity and Acceleration
When working with three dimensional dynamic systems it is important to have an expression for the absolute angular velocity vector for a rigid body in order to be able to write an expression for its angular momentum vector. The angular momentum is required for moment balances.
Relative angular velocity vectors can be added together in the same way that relative velocity vectors were in Section 1.5. That is, having established the angular velocity of one body in a chain of bodies with respect to a stationary body (i.e. the absolute angular velocity of the body), we simply go through the chain adding the relative angular velocity of neighboring bodies as we pass through the joints connecting them.
For example, the absolute angular velocity of body 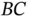 in Figure 1.5can be determined as follows,
in Figure 1.5can be determined as follows,
(1.37) 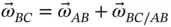
where the joint at 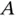 constrains
constrains 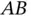 to rotate about a vertical axis relative to the ground, so that,
to rotate about a vertical axis relative to the ground, so that,
(1.38) 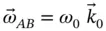
is the absolute angular velocity of 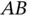 . The joint at
. The joint at  constrains
constrains 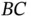 to rotate about the axis of
to rotate about the axis of 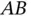 with an angular velocity that is relative to
with an angular velocity that is relative to 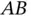 giving,
giving,
(1.39) 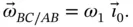
Substituting Equations 1.38and 1.39into Equation 1.37gives the absolute angular velocity of 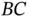
(1.40) 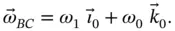
The absolute angular acceleration of 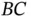 is, by definition, the time rate of change of the absolute angular velocity vector of
is, by definition, the time rate of change of the absolute angular velocity vector of 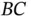 . In this example we note that the angular velocity vector is expressed in a rotating coordinate system so that there will be both a rate of change of magnitude and a rate of change of direction. The coordinate system has angular velocity
. In this example we note that the angular velocity vector is expressed in a rotating coordinate system so that there will be both a rate of change of magnitude and a rate of change of direction. The coordinate system has angular velocity 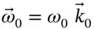 . Using the symbol
. Using the symbol 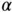 for angular acceleration we can write,
for angular acceleration we can write,
(1.41) 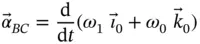
which becomes, upon differentiation,
(1.42) 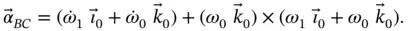
The final result, after performing the cross‐multiplication in Equation 1.42, is that the absolute angular acceleration of 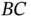 is,
is,
(1.43) 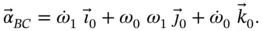
1.7 The General Acceleration Expression
In Section 1.4 we derived an acceleration expression for a very specific example. The final result (shown in Equation 1.20) has an interesting and, perhaps, unexpected form. In particular, the origin of the term that has twice the product of an angular velocity and a translational velocity (i.e. 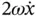 ) is not immediately obvious. The origin of all of the acceleration terms in a general expression like that in Equation 1.20is described below. The description is offered twice – first in a mathematical form then in a graphical form.
) is not immediately obvious. The origin of all of the acceleration terms in a general expression like that in Equation 1.20is described below. The description is offered twice – first in a mathematical form then in a graphical form.
In general, the derivation of an expression for the acceleration of a point (say 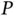 ) relative to another point (say
) relative to another point (say 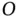 ) starts with the position vector of
) starts with the position vector of 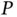 with respect to
with respect to 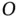 and then differentiates it twice. Each differentiation must take account of the angular velocity of the coordinate system being used to express the vectors.
and then differentiates it twice. Each differentiation must take account of the angular velocity of the coordinate system being used to express the vectors.
Let the position vector be
(1.44) 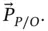
Then, applying Equation 1.6, the velocity is,
(1.45) 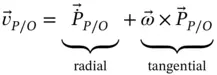
Читать дальше

 . That is,
. That is,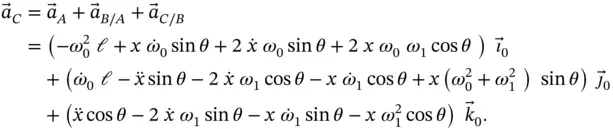
 in Figure 1.5can be determined as follows,
in Figure 1.5can be determined as follows,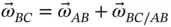
 constrains
constrains 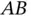 to rotate about a vertical axis relative to the ground, so that,
to rotate about a vertical axis relative to the ground, so that,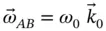
 . The joint at
. The joint at  constrains
constrains  to rotate about the axis of
to rotate about the axis of 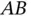 with an angular velocity that is relative to
with an angular velocity that is relative to 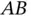 giving,
giving,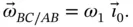
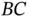
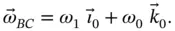
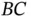 is, by definition, the time rate of change of the absolute angular velocity vector of
is, by definition, the time rate of change of the absolute angular velocity vector of 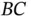 . In this example we note that the angular velocity vector is expressed in a rotating coordinate system so that there will be both a rate of change of magnitude and a rate of change of direction. The coordinate system has angular velocity
. In this example we note that the angular velocity vector is expressed in a rotating coordinate system so that there will be both a rate of change of magnitude and a rate of change of direction. The coordinate system has angular velocity 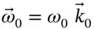 . Using the symbol
. Using the symbol 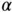 for angular acceleration we can write,
for angular acceleration we can write,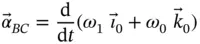
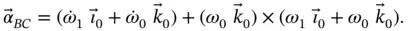
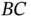 is,
is,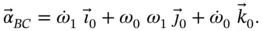
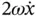 ) is not immediately obvious. The origin of all of the acceleration terms in a general expression like that in Equation 1.20is described below. The description is offered twice – first in a mathematical form then in a graphical form.
) is not immediately obvious. The origin of all of the acceleration terms in a general expression like that in Equation 1.20is described below. The description is offered twice – first in a mathematical form then in a graphical form.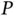 ) relative to another point (say
) relative to another point (say 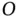 ) starts with the position vector of
) starts with the position vector of 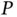 with respect to
with respect to 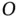 and then differentiates it twice. Each differentiation must take account of the angular velocity of the coordinate system being used to express the vectors.
and then differentiates it twice. Each differentiation must take account of the angular velocity of the coordinate system being used to express the vectors.