(1.11) 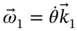
and the velocity of  relative to
relative to  is therefore 4 ,
is therefore 4 ,
(1.12) 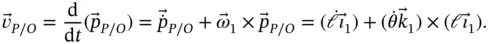
Since 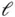 is constant,
is constant, 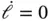 , and the final result is,
, and the final result is,
(1.13) 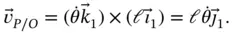
We now have two expressions for 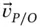 ( Equations 1.9and 1.13). Since there can only be one value of this relative velocity, the two expressions must be equal to each other. However, the use of two different coordinate systems makes them look different. In order to compare them, we must be able to transform results from one coordinate system to the other.
( Equations 1.9and 1.13). Since there can only be one value of this relative velocity, the two expressions must be equal to each other. However, the use of two different coordinate systems makes them look different. In order to compare them, we must be able to transform results from one coordinate system to the other.
Keep in mind that sequential sets of unit vectors are related to each other by simple plane rotations. Also note that the unit vectors are not related to any point in the system – they simply express directions. Given these two facts, we can relate the two sets of unit vectors we have been using by noting that 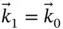 (i.e. the plane rotation relating the two sets is a rotation about the
(i.e. the plane rotation relating the two sets is a rotation about the 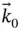 or
or 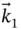 axis). The relationships between the two sets of unit vectors can be expressed as follows.
axis). The relationships between the two sets of unit vectors can be expressed as follows.
(1.14) 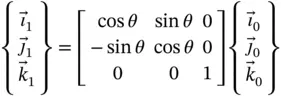
or
(1.15) 
The first transformation ( Equation 1.14) can be used with Equation 1.13to show that,
(1.16) 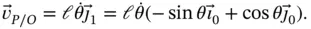
This is the same result as that shown in Equation 1.9.
Similarly, the second transformation ( Equation 1.15) can be used with Equation 1.9to show that,
(1.17) 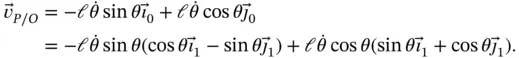
Expanding this yields,
(1.18) 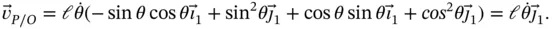
This is the same result as that shown in Equation 1.13.
The transformations described in this example are typical of those used in dynamic analysis. Dynamicists are prone to using whatever coordinate system is appropriate at the time and, sometimes, there are many intermediate coordinate systems used in deriving the final system. Nevertheless, each coordinate system in the sequence must be right handed and must be generated by a simple plane rotation from the preceding system.
1.4 Two Dimensional Motion with Variable Length
Figure 1.4shows a rigid body rotating in a plane about a fixed point 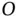 . The body has a slot cut in it and a small object
. The body has a slot cut in it and a small object 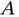 slides in this slot. Expressions for the velocity and acceleration of
slides in this slot. Expressions for the velocity and acceleration of 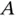 are desired.
are desired.

Figure 1.4A slider in a slot.
Since the distance from 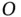 to
to 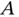 changes with time, we start by defining a variable distance
changes with time, we start by defining a variable distance 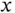 from
from 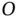 to
to 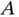 . A set of rotating unit vectors (
. A set of rotating unit vectors ( 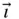 ,
, 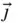 ,
, 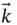 ), fixed in the rotating body, as shown, is appropriate for this analysis since the position vector
), fixed in the rotating body, as shown, is appropriate for this analysis since the position vector 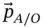 is aligned with
is aligned with 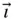 , thereby making it easy to write.
, thereby making it easy to write.
The angular velocity of the body is not specified in magnitude but the fact that the body rotates in a plane fixes the direction of the angular velocity to be 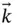 . We assume that the angular velocity is,
. We assume that the angular velocity is,

where 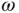 is not constant so that
is not constant so that  (i.e. the rate of change of magnitude of the angular velocity vector) exists.
(i.e. the rate of change of magnitude of the angular velocity vector) exists.
Читать дальше

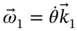
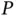 relative to
relative to 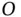 is therefore 4 ,
is therefore 4 ,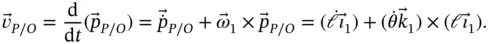
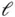 is constant,
is constant, 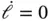 , and the final result is,
, and the final result is,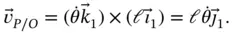
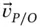 ( Equations 1.9and 1.13). Since there can only be one value of this relative velocity, the two expressions must be equal to each other. However, the use of two different coordinate systems makes them look different. In order to compare them, we must be able to transform results from one coordinate system to the other.
( Equations 1.9and 1.13). Since there can only be one value of this relative velocity, the two expressions must be equal to each other. However, the use of two different coordinate systems makes them look different. In order to compare them, we must be able to transform results from one coordinate system to the other.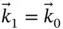 (i.e. the plane rotation relating the two sets is a rotation about the
(i.e. the plane rotation relating the two sets is a rotation about the 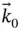 or
or 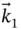 axis). The relationships between the two sets of unit vectors can be expressed as follows.
axis). The relationships between the two sets of unit vectors can be expressed as follows.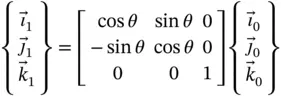

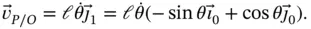
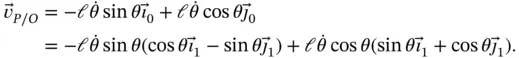
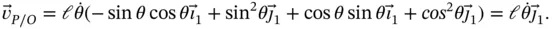
 . The body has a slot cut in it and a small object
. The body has a slot cut in it and a small object 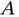 slides in this slot. Expressions for the velocity and acceleration of
slides in this slot. Expressions for the velocity and acceleration of  are desired.
are desired.
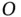 to
to 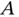 changes with time, we start by defining a variable distance
changes with time, we start by defining a variable distance 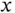 from
from 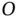 to
to 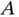 . A set of rotating unit vectors (
. A set of rotating unit vectors ( 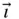 ,
, 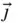 ,
, 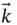 ), fixed in the rotating body, as shown, is appropriate for this analysis since the position vector
), fixed in the rotating body, as shown, is appropriate for this analysis since the position vector 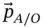 is aligned with
is aligned with 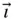 , thereby making it easy to write.
, thereby making it easy to write.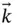 . We assume that the angular velocity is,
. We assume that the angular velocity is,
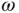 is not constant so that
is not constant so that  (i.e. the rate of change of magnitude of the angular velocity vector) exists.
(i.e. the rate of change of magnitude of the angular velocity vector) exists.










