Ronald J. Anderson - The Practice of Engineering Dynamics

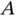The position of with respect to 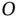is then,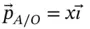

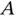and, differentiating this, we find the velocity of with respect to 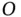to be,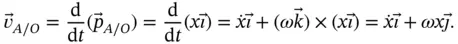

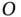(1.19)

The acceleration of the slider relative to point is defined to be,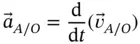

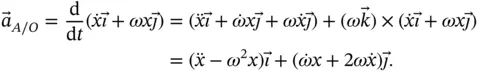
or

(1.20)

Since both the velocity and the acceleration 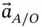are relative to the fixed or inertial point 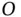, they are in fact the absolute velocity and acceleration of point 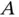. We commonly write absolute velocities and accelerations without subscripts yielding,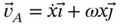

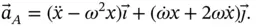
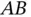(1.21)

and

(1.22)

Figure 1.5shows a three degree of freedom robot. The horizontal arm is of fixed length 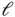and is free to rotate about a vertical axis through point 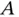with angular speed 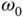. Arm 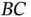has a variable length 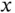and is free to rotate about an axis passing through points 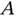and 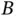with angular speed 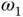. The end effector is located at point 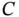. Of interest for the kinematic analysis are expressions for the absolute velocity and acceleration of the end effector.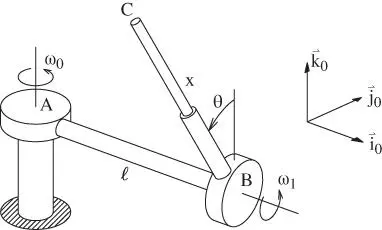

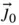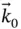Figure 1.5A three dimensional robot.

As a first step we define the right handed coordinate system ( , , ) fixed in the arm 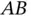. This is a rotating coordinate system with angular velocity .

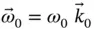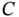The process of finding the absolute velocity and acceleration of point is just as outlined in Section 1.2. The first step is to find a fixed point. In this system, point 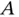serves the purpose as it has no velocity or acceleration.

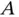The next step is to define a position vector that goes from to 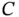. This is the vector 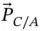shown in Figure 1.6. Notice that it goes through space from 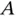to and its rate of change cannot be described directly using the motions of the physical components of the system.

Figure 1.6Relative position vectors.

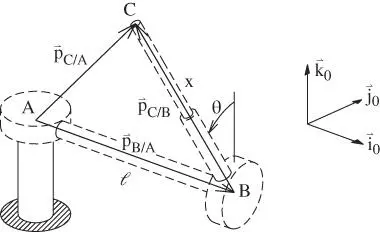
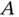We must, in fact, work with relative position vectors that go from the fixed point to the point of interest by passing from joint to joint. In this case, we define first a vector that goes from to 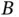( 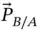) and then add to it a vector that goes from 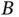to 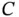( 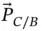). That is,