(1.23) 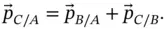
By definition, the absolute velocity of 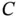 is the time rate of change of its position with respect to a fixed point. That is,
is the time rate of change of its position with respect to a fixed point. That is,
(1.24) 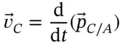
which, upon substitution of Equation 1.23, becomes,
(1.25) 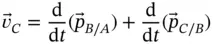
which in turn becomes,
(1.26) 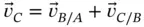
where we see that the absolute velocity of 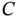 can be expressed as the sum of the velocities of points in the vector chain relative to previous points in the chain so long as the first point is stationary.
can be expressed as the sum of the velocities of points in the vector chain relative to previous points in the chain so long as the first point is stationary.
Simply differentiating Equation 1.26with respect to time gives the corresponding expression for accelerations.
(1.27) 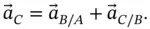
With respect to the particular system being considered here, we can write,
(1.28) 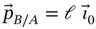
and,
(1.29) 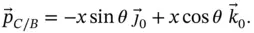
Considering first the position of 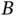 with respect to
with respect to 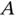 we see that the length
we see that the length 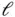 is constant so there will be no rate of change of magnitude of the vector but there will be a rate of change of direction since the coordinate system is rotating. We find,
is constant so there will be no rate of change of magnitude of the vector but there will be a rate of change of direction since the coordinate system is rotating. We find,
(1.30) 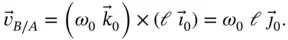
We differentiate again, noting that 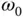 is not constant so that there will be a rate of change of magnitude this time, and find,
is not constant so that there will be a rate of change of magnitude this time, and find,
(1.31) 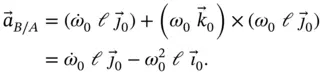
The rate of change of 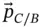 is a little more complicated for two reasons. First, the vector is not in the body to which the coordinate system being used is fixed so there will be a rate of change of magnitude arising from the time derivatives of the trigonometric functions. Second, the vector itself is not of fixed length so terms involving the rate of change of
is a little more complicated for two reasons. First, the vector is not in the body to which the coordinate system being used is fixed so there will be a rate of change of magnitude arising from the time derivatives of the trigonometric functions. Second, the vector itself is not of fixed length so terms involving the rate of change of 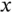 will appear. Differentiating yields,
will appear. Differentiating yields,
(1.32) 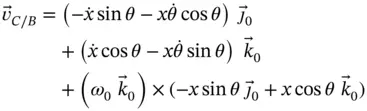
which, noting that 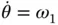 (see Figure 1.5), expands to,
(see Figure 1.5), expands to,
(1.33) 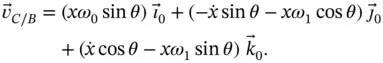
Finally, we differentiate 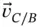 to get
to get 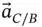 as follows.
as follows.
(1.34) 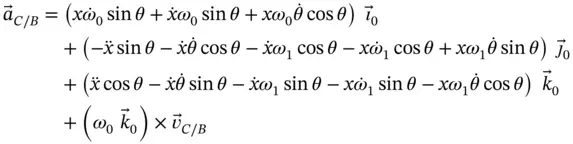
which, after considerable effort and again noting that 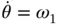 , expands to,
, expands to,
(1.35) 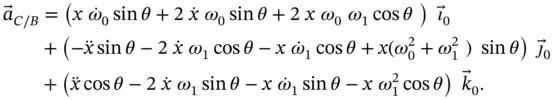
If you have worked through the derivation of Equation 1.35you will be aware that the probability of making a mistake when deriving equations such as this is high. A quick, approximate check on the accuracy of your work can be made by verifying that every term in the acceleration expression has dimensions of acceleration or, more simply, contains two derivatives of displacement variables. That is, terms like 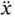 are obviously accelerations whereas terms like
are obviously accelerations whereas terms like 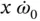 might require a little thought before realizing that
might require a little thought before realizing that 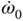 is the second derivative of an angle and must be scaled by a length, in this case
is the second derivative of an angle and must be scaled by a length, in this case 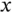 , in order to be a translational acceleration. Products of angular velocities such as
, in order to be a translational acceleration. Products of angular velocities such as 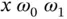 and
and 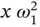 have two derivatives of angles multiplied together and are again scaled by a length,
have two derivatives of angles multiplied together and are again scaled by a length, 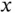 , to become translational accelerations. In addition, it is somewhat comforting to see several terms that have the Coriolis factor of 2 associated with them. Suspicion should be raised when factors other than 1 or 2 are seen in acceleration expressions.
, to become translational accelerations. In addition, it is somewhat comforting to see several terms that have the Coriolis factor of 2 associated with them. Suspicion should be raised when factors other than 1 or 2 are seen in acceleration expressions.
Читать дальше

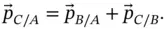
 is the time rate of change of its position with respect to a fixed point. That is,
is the time rate of change of its position with respect to a fixed point. That is,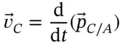
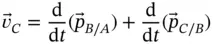
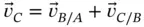
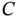 can be expressed as the sum of the velocities of points in the vector chain relative to previous points in the chain so long as the first point is stationary.
can be expressed as the sum of the velocities of points in the vector chain relative to previous points in the chain so long as the first point is stationary.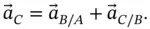
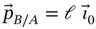
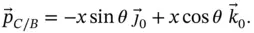
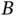 with respect to
with respect to 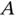 we see that the length
we see that the length 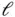 is constant so there will be no rate of change of magnitude of the vector but there will be a rate of change of direction since the coordinate system is rotating. We find,
is constant so there will be no rate of change of magnitude of the vector but there will be a rate of change of direction since the coordinate system is rotating. We find,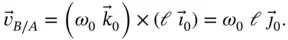
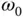 is not constant so that there will be a rate of change of magnitude this time, and find,
is not constant so that there will be a rate of change of magnitude this time, and find,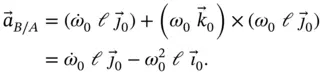
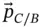 is a little more complicated for two reasons. First, the vector is not in the body to which the coordinate system being used is fixed so there will be a rate of change of magnitude arising from the time derivatives of the trigonometric functions. Second, the vector itself is not of fixed length so terms involving the rate of change of
is a little more complicated for two reasons. First, the vector is not in the body to which the coordinate system being used is fixed so there will be a rate of change of magnitude arising from the time derivatives of the trigonometric functions. Second, the vector itself is not of fixed length so terms involving the rate of change of 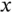 will appear. Differentiating yields,
will appear. Differentiating yields,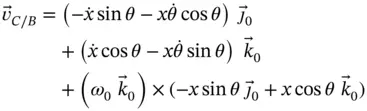
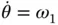 (see Figure 1.5), expands to,
(see Figure 1.5), expands to,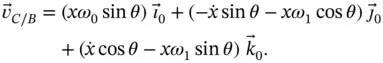
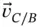 to get
to get 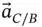 as follows.
as follows.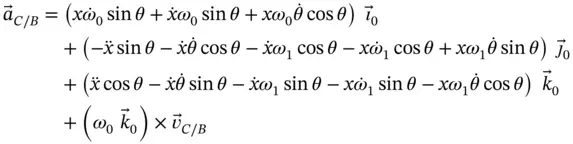
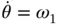 , expands to,
, expands to,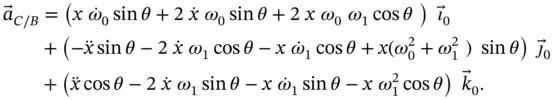
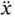 are obviously accelerations whereas terms like
are obviously accelerations whereas terms like 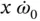 might require a little thought before realizing that
might require a little thought before realizing that 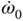 is the second derivative of an angle and must be scaled by a length, in this case
is the second derivative of an angle and must be scaled by a length, in this case 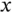 , in order to be a translational acceleration. Products of angular velocities such as
, in order to be a translational acceleration. Products of angular velocities such as 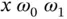 and
and 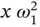 have two derivatives of angles multiplied together and are again scaled by a length,
have two derivatives of angles multiplied together and are again scaled by a length, 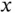 , to become translational accelerations. In addition, it is somewhat comforting to see several terms that have the Coriolis factor of 2 associated with them. Suspicion should be raised when factors other than 1 or 2 are seen in acceleration expressions.
, to become translational accelerations. In addition, it is somewhat comforting to see several terms that have the Coriolis factor of 2 associated with them. Suspicion should be raised when factors other than 1 or 2 are seen in acceleration expressions.










