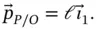1.2 Performing Kinematic Analysis
Before proceeding with examples of kinematic analyses we state here the steps that are necessary in achieving a successful result. This first step in any dynamic analysis is vitally important. The goal is to derive expressions for the absolute velocities and accelerations of the centers of mass of the bodies making up the system being analyzed. In addition, expressions for the absolute angular velocities and angular accelerations of the bodies will be required. It is at this first step of the analysis that degrees of freedom are defined and constraints on relative motion between bodies are satisfied.
For this general description of kinematic analysis, we assume that we are analyzing a system that has multiple bodies connected to each other by joints and that we are attempting to derive an expression for the acceleration of the center of mass of a body that is not the first in the assembly.
The procedure is as follows.
1 Find a fixed point (i.e. one having no velocity or acceleration) in the system from which you can begin to write relative position vectors that will lead to the centers of mass of bodies in the system.
2 Define a position vector that goes from the fixed point, through the first body, to the next joint in the system. This is the position of the joint relative to the fixed point.
3 Determine how many degrees of freedom, both translational and rotational, are required to define the motion of the relative position vector just defined. The degrees of freedom must be chosen to satisfy the constraints imposed by the joint that connects this body to ground.
4 Define a coordinate system in which the relative position vector will be written and determine the angular velocity of the coordinate system.
5 Repeat the previous three steps as you go from joint to joint in the system, always being careful to satisfy the joint constraints by defining appropriate degrees of freedom.
6 When the desired body is reached, define a final relative position vector from the joint to the center of mass.
7 The sum of all the relative position vectors will be the absolute position of the center of mass and the derivatives of the sum of vectors will yield the absolute velocity and acceleration of the center of mass.
1.3 Two Dimensional Motion with Constant Length
Figure 1.3shows a rigid rod of length, 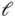 , rotating about a fixed point,
, rotating about a fixed point, 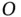 , in a plane. An expression for the velocity of the free end of the rod,
, in a plane. An expression for the velocity of the free end of the rod, 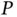 , relative to point
, relative to point  is desired.
is desired.
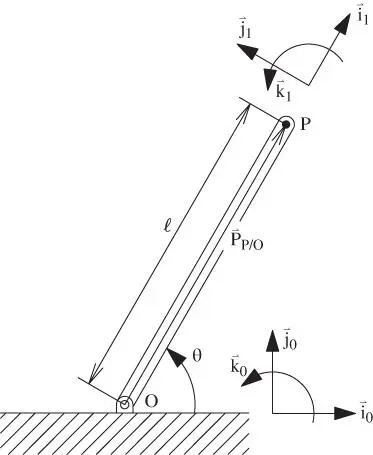
Figure 1.3A rigid rod rotating about a fixed point.
By definition, the velocity of  relative to
relative to  is the time derivative of the position of
is the time derivative of the position of 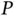 relative to
relative to 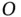 . This position vector is designated
. This position vector is designated 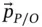 and is shown in the figure.
and is shown in the figure.
In order to differentiate the position vector, we must have an expression for it and this means we must first choose a coordinate system 3 in which to work. For a start, we can choose a right handed coordinate system fixed in the ground. The set of unit vectors 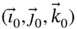 is such a system. The angular velocity of this coordinate system is zero (i.e.
is such a system. The angular velocity of this coordinate system is zero (i.e. 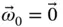 ) since it is fixed in the ground.
) since it is fixed in the ground.
An expression for the position of 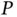 relative to
relative to 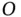 in this system is,
in this system is,
(1.7) 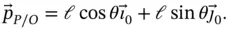
We apply Equation 1.6to 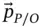 to get,
to get,
(1.8) 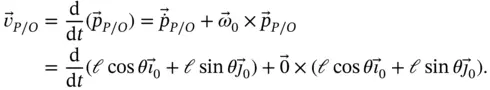
In this coordinate system, it is clear that there is a rate of change of magnitude of the vector only and the velocity of point 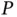 relative to
relative to 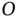 after performing the simple differentiation is,
after performing the simple differentiation is,
(1.9) 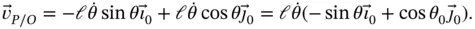
Another derivation of the velocity of 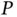 relative to
relative to 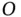 might use the system of unit vectors
might use the system of unit vectors 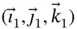 that are fixed in the rod. The advantage of using this system is that the position vector is easily expressed as,
that are fixed in the rod. The advantage of using this system is that the position vector is easily expressed as,
(1.10) 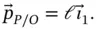
Note that the length of this vector is a constant so that the total derivative must come from its rate of change of direction. The angular velocity of the coordinate system is equal to the angular velocity of the rod since the coordinate system is fixed in the rod. That is,
Читать дальше

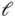 , rotating about a fixed point,
, rotating about a fixed point, 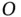 , in a plane. An expression for the velocity of the free end of the rod,
, in a plane. An expression for the velocity of the free end of the rod, 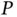 , relative to point
, relative to point 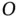 is desired.
is desired.
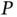 relative to
relative to 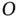 is the time derivative of the position of
is the time derivative of the position of 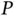 relative to
relative to 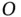 . This position vector is designated
. This position vector is designated 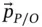 and is shown in the figure.
and is shown in the figure.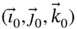 is such a system. The angular velocity of this coordinate system is zero (i.e.
is such a system. The angular velocity of this coordinate system is zero (i.e. 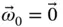 ) since it is fixed in the ground.
) since it is fixed in the ground.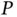 relative to
relative to 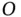 in this system is,
in this system is,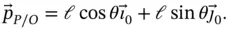
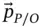 to get,
to get,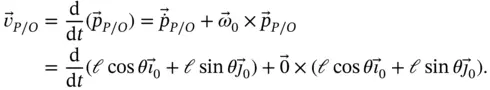
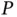 relative to
relative to 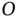 after performing the simple differentiation is,
after performing the simple differentiation is,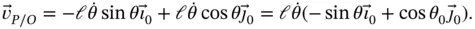
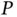 relative to
relative to 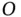 might use the system of unit vectors
might use the system of unit vectors 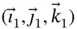 that are fixed in the rod. The advantage of using this system is that the position vector is easily expressed as,
that are fixed in the rod. The advantage of using this system is that the position vector is easily expressed as,