1 Choose the model that minimizes . In case of tied values, the simplest model (smallest ) would be chosen. In these data, this rule implies choosing .
An additional operational rule for the use of 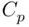 has been suggested. When a particular model contains all of the necessary predictors, the residual mean square for the model should be roughly equal to
has been suggested. When a particular model contains all of the necessary predictors, the residual mean square for the model should be roughly equal to 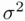 . Since the model that includes all of the predictors should also include all of the necessary ones,
. Since the model that includes all of the predictors should also include all of the necessary ones, 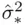 should also be roughly equal to
should also be roughly equal to 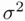 . This implies that if a model includes all of the necessary predictors, then
. This implies that if a model includes all of the necessary predictors, then
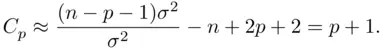
This suggests the following model selection rule:
1 Choose the simplest model such that or smaller. In these data, this rule implies choosing .
A weakness of the 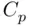 criterion is that its value depends on the largest set of candidate predictors (through
criterion is that its value depends on the largest set of candidate predictors (through 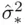 ), which means that adding predictors that provide no predictive power to the set of candidate models can change the choice of best model. A general approach that avoids this is through the use of statistical information. A detailed discussion of the determination of information measures is beyond the scope of this book, but Burnham and Anderson (2002) provides extensive discussion of the topic. The Akaike Information Criterion
), which means that adding predictors that provide no predictive power to the set of candidate models can change the choice of best model. A general approach that avoids this is through the use of statistical information. A detailed discussion of the determination of information measures is beyond the scope of this book, but Burnham and Anderson (2002) provides extensive discussion of the topic. The Akaike Information Criterion 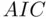 , introduced by Akaike (1973),
, introduced by Akaike (1973),
(2.2) 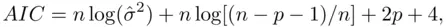
where the 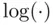 function refers to natural logs, is such a measure, and it estimates the information lost in approximating the true model by a candidate model. It is clear from (2.2)that minimizing
function refers to natural logs, is such a measure, and it estimates the information lost in approximating the true model by a candidate model. It is clear from (2.2)that minimizing 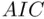 achieves the goal of balancing strength of fit with simplicity, and because of the
achieves the goal of balancing strength of fit with simplicity, and because of the 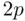 term in the criterion this will result in the choice of similar models as when minimizing
term in the criterion this will result in the choice of similar models as when minimizing 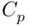 . It is well known that
. It is well known that 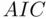 has a tendency to lead to overfitting, particularly in small samples. That is, the penalty term in
has a tendency to lead to overfitting, particularly in small samples. That is, the penalty term in 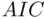 designed to guard against too complicated a model is not strong enough. A modified version of
designed to guard against too complicated a model is not strong enough. A modified version of 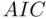 that helps address this problem is the corrected
that helps address this problem is the corrected 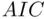 ,
,
(2.3) 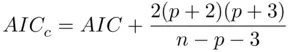
(Hurvich and Tsai, 1989). Equation (2.3)shows that (especially for small samples) models with fewer parameters will be more strongly preferred when minimizing 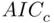 than when minimizing
than when minimizing 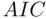 , providing stronger protection against overfitting. In large samples, the two criteria are virtually identical, but in small samples, or when considering models with a large number of parameters,
, providing stronger protection against overfitting. In large samples, the two criteria are virtually identical, but in small samples, or when considering models with a large number of parameters, 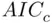 is the better choice. This suggests the following model selection rule:
is the better choice. This suggests the following model selection rule:
1 Choose the model that minimizes . In case of tied values, the simplest model (smallest ) would be chosen. In these data, this rule implies choosing , although the value for is virtually identical to that of . Note that the overall level of the values is not meaningful, and should not be compared to values or values for other data sets; it is only the value for a model for a given data set relative to the values of others for that data set that matter.
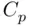 ,
, 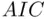 , and
, and  have the desirable property that they are efficient model selection criteria. This means that in the (realistic) situation where the set of candidate models does not include the “true” model (that is, a good model is just viewed as a useful approximation to reality), as the sample gets larger the error obtained in making predictions using the model chosen using these criteria becomes indistinguishable from the error obtained using the best possible model among all candidate models. That is, in this large‐sample predictive sense, it is as if the best approximation was known to the data analyst. Another well‐known criterion, the Bayesian Information Criterion
have the desirable property that they are efficient model selection criteria. This means that in the (realistic) situation where the set of candidate models does not include the “true” model (that is, a good model is just viewed as a useful approximation to reality), as the sample gets larger the error obtained in making predictions using the model chosen using these criteria becomes indistinguishable from the error obtained using the best possible model among all candidate models. That is, in this large‐sample predictive sense, it is as if the best approximation was known to the data analyst. Another well‐known criterion, the Bayesian Information Criterion 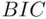 [which substitutes
[which substitutes 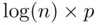 for
for 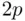 in (2.2)], does not have this property, but is instead a consistent criterion. Such a criterion has the property that if the “true” model is in fact among the candidate models the criterion will select that model with probability approaching
in (2.2)], does not have this property, but is instead a consistent criterion. Such a criterion has the property that if the “true” model is in fact among the candidate models the criterion will select that model with probability approaching 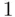 as the sample size increases. Thus,
as the sample size increases. Thus, 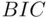 is a more natural criterion to use if the goal is to identify the “true” predictors with nonzero slopes (which of course presumes that there are such things as “true” predictors in a “true” model).
is a more natural criterion to use if the goal is to identify the “true” predictors with nonzero slopes (which of course presumes that there are such things as “true” predictors in a “true” model). 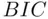 will generally choose simpler models than
will generally choose simpler models than  because of its stronger penalty (
because of its stronger penalty (  for
for 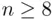 ), and a version
), and a version 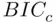 that adjusts
that adjusts 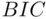 as in (2.3)leads to even simpler models. This supports the notion that from a predictive point of view including a few unnecessary predictors (overfitting) is far less damaging than is omitting necessary predictors (underfitting).
as in (2.3)leads to even simpler models. This supports the notion that from a predictive point of view including a few unnecessary predictors (overfitting) is far less damaging than is omitting necessary predictors (underfitting).
Читать дальше

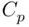 has been suggested. When a particular model contains all of the necessary predictors, the residual mean square for the model should be roughly equal to
has been suggested. When a particular model contains all of the necessary predictors, the residual mean square for the model should be roughly equal to 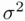 . Since the model that includes all of the predictors should also include all of the necessary ones,
. Since the model that includes all of the predictors should also include all of the necessary ones, 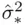 should also be roughly equal to
should also be roughly equal to 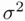 . This implies that if a model includes all of the necessary predictors, then
. This implies that if a model includes all of the necessary predictors, then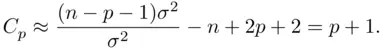
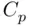 criterion is that its value depends on the largest set of candidate predictors (through
criterion is that its value depends on the largest set of candidate predictors (through 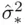 ), which means that adding predictors that provide no predictive power to the set of candidate models can change the choice of best model. A general approach that avoids this is through the use of statistical information. A detailed discussion of the determination of information measures is beyond the scope of this book, but Burnham and Anderson (2002) provides extensive discussion of the topic. The Akaike Information Criterion
), which means that adding predictors that provide no predictive power to the set of candidate models can change the choice of best model. A general approach that avoids this is through the use of statistical information. A detailed discussion of the determination of information measures is beyond the scope of this book, but Burnham and Anderson (2002) provides extensive discussion of the topic. The Akaike Information Criterion 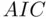 , introduced by Akaike (1973),
, introduced by Akaike (1973),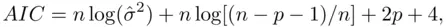
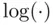 function refers to natural logs, is such a measure, and it estimates the information lost in approximating the true model by a candidate model. It is clear from (2.2)that minimizing
function refers to natural logs, is such a measure, and it estimates the information lost in approximating the true model by a candidate model. It is clear from (2.2)that minimizing 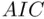 achieves the goal of balancing strength of fit with simplicity, and because of the
achieves the goal of balancing strength of fit with simplicity, and because of the 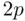 term in the criterion this will result in the choice of similar models as when minimizing
term in the criterion this will result in the choice of similar models as when minimizing 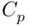 . It is well known that
. It is well known that 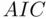 has a tendency to lead to overfitting, particularly in small samples. That is, the penalty term in
has a tendency to lead to overfitting, particularly in small samples. That is, the penalty term in 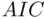 designed to guard against too complicated a model is not strong enough. A modified version of
designed to guard against too complicated a model is not strong enough. A modified version of 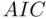 that helps address this problem is the corrected
that helps address this problem is the corrected 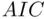 ,
,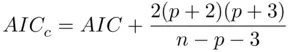
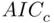 than when minimizing
than when minimizing 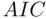 , providing stronger protection against overfitting. In large samples, the two criteria are virtually identical, but in small samples, or when considering models with a large number of parameters,
, providing stronger protection against overfitting. In large samples, the two criteria are virtually identical, but in small samples, or when considering models with a large number of parameters, 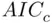 is the better choice. This suggests the following model selection rule:
is the better choice. This suggests the following model selection rule: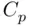 ,
, 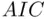 , and
, and  have the desirable property that they are efficient model selection criteria. This means that in the (realistic) situation where the set of candidate models does not include the “true” model (that is, a good model is just viewed as a useful approximation to reality), as the sample gets larger the error obtained in making predictions using the model chosen using these criteria becomes indistinguishable from the error obtained using the best possible model among all candidate models. That is, in this large‐sample predictive sense, it is as if the best approximation was known to the data analyst. Another well‐known criterion, the Bayesian Information Criterion
have the desirable property that they are efficient model selection criteria. This means that in the (realistic) situation where the set of candidate models does not include the “true” model (that is, a good model is just viewed as a useful approximation to reality), as the sample gets larger the error obtained in making predictions using the model chosen using these criteria becomes indistinguishable from the error obtained using the best possible model among all candidate models. That is, in this large‐sample predictive sense, it is as if the best approximation was known to the data analyst. Another well‐known criterion, the Bayesian Information Criterion 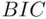 [which substitutes
[which substitutes 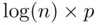 for
for 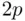 in (2.2)], does not have this property, but is instead a consistent criterion. Such a criterion has the property that if the “true” model is in fact among the candidate models the criterion will select that model with probability approaching
in (2.2)], does not have this property, but is instead a consistent criterion. Such a criterion has the property that if the “true” model is in fact among the candidate models the criterion will select that model with probability approaching 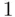 as the sample size increases. Thus,
as the sample size increases. Thus, 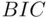 is a more natural criterion to use if the goal is to identify the “true” predictors with nonzero slopes (which of course presumes that there are such things as “true” predictors in a “true” model).
is a more natural criterion to use if the goal is to identify the “true” predictors with nonzero slopes (which of course presumes that there are such things as “true” predictors in a “true” model). 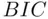 will generally choose simpler models than
will generally choose simpler models than  because of its stronger penalty (
because of its stronger penalty (  for
for 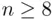 ), and a version
), and a version 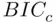 that adjusts
that adjusts 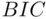 as in (2.3)leads to even simpler models. This supports the notion that from a predictive point of view including a few unnecessary predictors (overfitting) is far less damaging than is omitting necessary predictors (underfitting).
as in (2.3)leads to even simpler models. This supports the notion that from a predictive point of view including a few unnecessary predictors (overfitting) is far less damaging than is omitting necessary predictors (underfitting).










