1 Cover
2 Title Page
3 Copyright
4 Dedication
5 Preface
6 About the Book
7 Introduction
8 Part I: Tensor Theory 1 Preliminaries1.1 Introduction 1.2 Systems of Different Orders 1.3 Summation Convention Certain Index 1.4 Kronecker Symbols 1.5 Linear Equations 1.6 Results on Matrices and Determinants of Systems 1.7 Differentiation of a Determinant 1.8 Examples 1.9 Exercises 2 Tensor Algebra2.1 Introduction 2.2 Scope of Tensor Analysis 2.3 Transformation of Coordinates in Sn 2.4 Transformation by Invariance 2.5 Transformation by Covariant Tensor and Contravariant Tensor 2.6 The Tensor Concept: Contravariant and Covariant Tensors 2.7 Algebra of Tensors 2.8 Symmetric and Skew-Symmetric Tensors 2.9 Outer Multiplication and Contraction 2.10 Quotient Law of Tensors 2.11 Reciprocal Tensor of a Tensor 2.12 Relative Tensor, Cartesian Tensor, Affine Tensor, and Isotropic Tensors 2.13 Examples 2.14 Exercises 3 Riemannian Metric3.1 Introduction 3.2 The Metric Tensor 3.3 Conjugate Tensor 3.4 Associated Tensors 3.5 Length of a Vector 3.6 Angle Between Two Vectors 3.7 Hypersurface 3.8 Angle Between Two Coordinate Hypersurfaces 3.9 Exercises 4 Tensor Calculus4.1 Introduction 4.2 Christoffel Symbols 4.3 Transformation of Christoffel Symbols 4.4 Covariant Differentiation of Tensor 4.5 Gradient, Divergence, and Curl 4.6 Exercises 5 Riemannian Geometry5.1 Introduction 5.2 Riemannian-Christoffel Tensor 5.3 Properties of Riemann-Christoffel Tensors 5.4 Ricci Tensor, Bianchi Identities, Einstein Tensors 5.5 Einstein Space 5.6 Riemannian and Euclidean Spaces 5.7 Exercises 6 The e-Systems and the Generalized Kronecker Deltas6.1 Introduction 6.2 e-Systems 6.3 Generalized Kronecker Delta 6.4 Contraction of 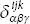 6.5 Application of e-Systems to Determinants and Tensor Characters of Generalized Kronecker Deltas 6.6 Exercises
6.5 Application of e-Systems to Determinants and Tensor Characters of Generalized Kronecker Deltas 6.6 Exercises
9 Part II: Differential Geometry 7 Curvilinear Coordinates in Space7.1 Introduction 7.2 Length of Arc 7.3 Curvilinear Coordinates in E 3 7.4 Reciprocal Base Systems 7.5 Partial Derivative 7.6 Exercises 8 Curves in Space8.1 Introduction 8.2 Intrinsic Differentiation 8.3 Parallel Vector Fields 8.4 Geometry of Space Curves 8.5 Serret-Frenet Formula 8.6 Equations of a Straight Line 8.7 Helix 8.8 Exercises 9 Intrinsic Geometry of Surfaces9.1 Introduction 9.2 Curvilinear Coordinates on a Surface 9.3 Intrinsic Geometry: First Fundamental Quadratic Form 9.4 Angle Between Two Intersecting Curves on a Surface 9.5 Geodesic in Rn 9.6 Geodesic Coordinates 9.7 Parallel Vectors on a Surface 9.8 Isometric Surface 9.9 The Riemannian–Christoffel Tensor and Gaussian Curvature 9.10 The Geodesic Curvature 9.11 Exercises 10 Surfaces in Space10.1 Introduction 10.2 The Tangent Vector 10.3 The Normal Line to the Surface 10.4 Tensor Derivatives 10.5 Second Fundamental Form of a Surface 10.6 The Integrability Condition 10.7 Formulas of Weingarten 10.8 Equations of Gauss and Codazzi 10.9 Mean and Total Curvatures of a Surface 10.10 Exercises 11 Curves on a Surface11.1 Introduction 11.2 Curve on a Surface: Theorem of Meusnier 11.3 The Principal Curvatures of a Surface 11.4 Rodrigue’s Formula 11.5 Exercises 12 Curvature of Surface12.1 Introduction 12.2 Surface of Positive and Negative Curvature 12.3 Parallel Surfaces 12.4 The Gauss-Bonnet Theorem 12.5 The n-Dimensional Manifolds 12.6 Hypersurfaces 12.7 Exercises
10 Part III: Analytical Mechanics 13 Classical Mechanics13.1 Introduction 13.2 Newtonian Laws of Motion 13.3 Equations of Motion of Particles 13.4 Conservative Force Field 13.5 Lagrangean Equations of Motion 13.6 Applications of Lagrangean Equations 13.7 Himilton’s Principle 13.8 Principle of Least Action 13.9 Generalized Coordinates 13.10 Lagrangean Equations in Generalized Coordinates 13.11 Divergence Theorem, Green’s Theorem, Laplacian Operator, and Stoke’s Theorem in Tensor Notation 13.12 Hamilton’s Canonical Equations 13.13 Exercises 14 Newtonian Law of Gravitations14.1 Introduction 14.2 Newtonian Laws of Gravitation 14.3 Theorem of Gauss 14.4 Poisson’s Equation 14.5 Solution of Poisson’s Equation 14.6 The Problem of Two Bodies 14.7 The Problem of Three Bodies 14.8 Exercises
11 Appendix A: Answers to Even-Numbered Exercises
12 References
13 Index
14 Also of Interest
15 End User License Agreement
1 Chapter 7Figure 7.1Figure 7.2Figure 7.3Figure 7.4Figure 7.5Figure 7.6Figure 7.7
2 Chapter 8Figure 8.1Figure 8.2Figure 8.3Figure 8.4
3 Chapter 9Figure 9.1Figure 9.2Figure 9.3Figure 9.4Figure 9.5
4 Chapter 10Figure 10.1
5 Chapter 11Figure 11.1Figure 11.2
6 Chapter 12Figure 12.1Figure 12.2
7 Chapter 13Figure 13.1Figure 13.2Figure 13.3Figure 13.4Figure 13.5
8 Chapter 14Figure 14.1Figure 14.2Figure 14.3
1 Cover
2 Table of Contents
3 Title Page
4 Copyright
5 Dedication
6 Preface
7 Begin Reading
8 Appendix A: Answers to Even-Numbered Exercises
9 References
10 Index
11 Also of Interest
12 End User License Agreement
1 vii
2 ii
3 iii
4 iv
5 v
6 xv
7 xvi
8 xvii
9 1
10 2
11 3
12 4
13 5
14 7
15 9
16 10
17 11
18 12
19 13
20 14
21 15
22 16
23 17
24 18
25 19
26 20
27 21
28 22
29 23
30 24
31 25
32 26
33 27
34 28
35 29
36 30
37 31
38 32
39 33
40 34
41 35
42 36
43 37
44 38
45 39
46 40
47 41
48 42
49 43
50 44
51 45
52 46
53 47
54 48
55 49
56 50
57 51
58 52
59 53
60 54
61 55
62 56
63 57
64 58
65 59
66 60
67 61
68 62
69 63
70 64
71 65
72 66
73 67
74 68
75 69
76 70
77 71
78 72
79 73
80 74
81 75
82 76
83 77
84 78
85 79
86 80
87 81
88 82
89 83
90 84
91 85
92 86
93 87
94 88
95 89
96 90
97 91
98 92
99 93
100 94
101 95
102 96
103 97
104 98
105 99
106 100
107 101
108 102
109 103
110 104
111 105
112 106
113 107
114 108
115 109
116 110
117 111
118 112
119 113
120 114
121 115
122 116
123 117
124 118
125 119
126 120
127 121
128 122
129 123
130 124
131 125
132 126
133 127
134 128
135 129
136 130
137 131
138 132
139 133
140 134
141 135
142 136
143 137
144 138
145 139
146 140
147 141
148 142
149 143
150 144
151 145
152 146
153 147
154 148
155 149
156 150
157 151
158 152
159 153
160 154
161 155
162 156
163 157
164 158
165 159
166 160
167 161
168 162
169 163
170 164
171 165
172 166
173 167
174 168
175 169
176 170
177 171
178 172
179 173
180 174
181 175
182 176
183 177
184 178
185 179
186 180
187 181
188 182
189 183
190 184
191 185
192 186
193 187
194 188
195 189
196 190
197 191
198 192
Читать дальше

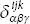 6.5 Application of e-Systems to Determinants and Tensor Characters of Generalized Kronecker Deltas 6.6 Exercises
6.5 Application of e-Systems to Determinants and Tensor Characters of Generalized Kronecker Deltas 6.6 Exercises










