We hope that this study is in the interest of researchers from a variety of mathematics, science, and engineering backgrounds and that Master level students will also be able to readily study more advanced concepts, such as properties of curves and surfaces, geometry of abstract manifolds, tensor analysis, and general relativity.
This book has three parts. The first part contains six chapters dealing with the calculus of tensors. In the first chapter, we deal with some preliminaries necessary for treatment of the materials in the succeeding chapters. In the second and third chapters, we discuss the algebra of tensors and metric tensors. Tensor calculus with Christoffel’s symbols and Riemannian Geometry are dealt with in the remaining chapters of this section. Part II contains six chapters discussing the applications of tensor calculus to geometry, mainly curves and surfaces in three-dimensional Euclidean space. The remaining two chapters in Part III mainly study Analytical Mechanics with tensor notation. At the end of each chapter, a large number of problems have been completely solved and exercises containing carefully motivated examples have been incorporated.
I would like to thank Professor Dr. Hanaa Hachimi and Dr. G. Suseedhran who gave me the scope and encouragement, with technical support, to write this book. I am also thankful to Professor Arindam Bhattacherya from Jadavpur University, India for offering some valuable suggestions for the improvement of this book.
Lastly, I wish to record my appreciation to the publishers and printers for their care and effort in bringing out this study in book form.
Dr. Dipankar De
Agartala, India
20 thApril 2021
An Introduction to Differential Geometry with Tensor Applications discusses the theory of tensor, curves, and surfaces and its application in Newtonian Mechanics. Since tensor analysis deals with entities and properties that are independent of choice of reference frames, it forms an ideal tool for the study of Differential Geometry and classical and celestial mechanics. This book provides a profound introduction to the basic theory of Differential Geometry: curves and surfaces. The author has tried to keep the treatment of the advanced material as lucid and comprehensive as possible mainly by including the utmost detailed calculations, numerous illustrative examples, and a wealth of complementing exercises with complete solutions making the book easily accessible even to beginners in the field. Differential Geometry, from the beginning on, characterizes the author’s utmost efficient didactical approach. This book is one of the outstanding standard primers of modern Differential Geometry and a basic source for a profound introductory course or as a highly recommendable reference for effective self-study of the subject.
Euclidean Geometry was one of the most important branches of mathematics for the last 2000 years. It was also the main tool used by scientists for the development of astronomy. In 300 B.C., Euclid treated geometry as a deductive system. In 1621, Sir Henry Savile raised some questions concerning what he called “two blemishes” in geometry: the theory of proportion and the theory of parallels. Euclid’s axiom of parallels (postulate V in the first book of Elements ) propagates that any two given lines in a plane, when produced indefinitely, will intersect if the sum of two interior angles made by a transversal with these lines is less than two right angles. In 1826, a Russian mathematician, Nicolai Lobachevski, presented a paper to the mathematician faculty of the University of Kazan based on the assumption that it is possible to draw through any point in a plane two lines parallel to a given line. Hungarian mathematician John Bolyai published some results in 1831, which, conceptually, have little difference from those of Lobachevski and perhaps it contains a deeper appreciation of the metric properties of space. However, it was only after Riemann’s profound dissertation on the hypotheses that the underlying foundations of geometry appeared posthumously in 1867, showing the importance of the metric concepts in geometry.
Riemann appeared to have been unaware of the work of Lobachevski and Bolyai, although it was well known to Gauss. Later, Beltrami published his classical paper on the interpretation of non-Euclidean geometries (1868) in which he analyzed the work of Lobachevski, Bolyai, and Riemann and stressed the fact that the metric properties of space are mere definitions. It appears that three consistent geometries are possible on surfaces of constant curvatures: Lobachevskian on a surface of constant negative curvature, Riemannian on a surface of constant positive curvature, and Euclidean on a surface of zero curvature. These geometries are called hyperbolic, elliptic, and parabolic, respectively.
Tensor calculus is concerned with the study of abstract objects, called tensors, which are independent of frames of reference used to describe them. In the early part of the 17 thcentury, geometry was developed by French mathematician Descartes. The great physicist W. Voigi discovered tensors and gave them this name in his remarkable book A Textbook of Crystal Physics published in 1910. Ricci and his student, Levi-cita, (1901) have been developing the subject of tensors, but it is well known that Einstein’s use of tensors as a tool in his general theory of relativity (1914) was mainly responsible for the sudden emergence of tensor calculus as a popular field of mathematical activities. The application of tensors in the field of mathematics and physics was mainly accelerated after the publication of Einstein’s famous paper The General Theory of Relativity .
Tensor is a generalization of the term vector and Tensor Calculus is a generalization of vector analysis. The concept of invariance of mathematical objects, under coordinate transformations, permeates the structure of tensor analysis to such an extent that it is important to get at the outset a clear notion of the particular brand of invariance we have in mind. In the given reference frame, a point P is determined by a set of coordinates, xi . If the coordinate system is changed, point P is described by a new set of coordinates, but the transformation of the coordinates does nothing to the point itself.
Here, we discuss how the term tensor may be considered as a generalization of the term vector.
We start with a two-dimensional Euclidean space, E 2, provided with a system of rectangular Cartesian coordinates. Let P and Q be two points of E 2, with ( x 1, x 2) and ( y 1, y 2) as their respective coordinates. Then, the coordinates of the directed line segment 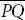 are ( x 1− y 1, x 2– y 2).
are ( x 1− y 1, x 2– y 2).
Denoting x 1− y 1 and x 2– y 2by z 1and z 2respectively, the coordinates of 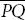 can be expressed as
can be expressed as
(0.1) 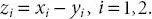
Next, we consider an orthogonal transformation of coordinate axes given by
(0.2) 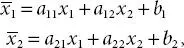
Читать дальше

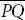 are ( x 1− y 1, x 2– y 2).
are ( x 1− y 1, x 2– y 2).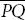 can be expressed as
can be expressed as