Introduction to Differential Geometry with Tensor Applications
Здесь есть возможность читать онлайн «Introduction to Differential Geometry with Tensor Applications» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Introduction to Differential Geometry with Tensor Applications
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:3 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Introduction to Differential Geometry with Tensor Applications: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Introduction to Differential Geometry with Tensor Applications»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
This is the only volume of its kind to explain, in precise and easy-to-understand language, the fundamentals of tensors and their applications in differential geometry and analytical mechanics with examples for practical applications and questions for use in a course setting.
This outstanding new volume: Introduction to Differential Geometry with Tensor Applications
Introduction to Differential Geometry with Tensor Applications

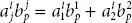 . Hence,
. Hence, 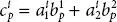 .
.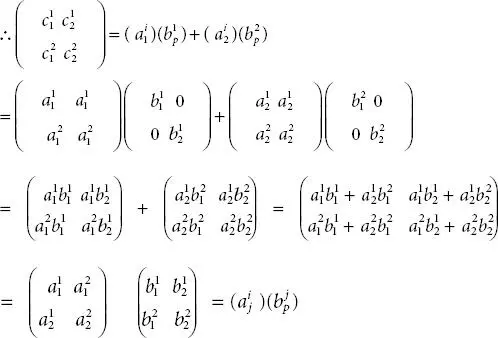
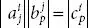 , as we know | AB | = | A || B |.
, as we know | AB | = | A || B |.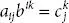 , then,
, then, 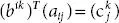 and
and 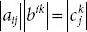 , where ( bik ) Tis the transpose of
, where ( bik ) Tis the transpose of 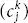
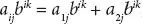 , hence,
, hence, 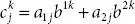 .
.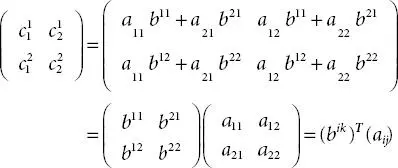
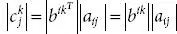 (since │ AT │ = │ A │).
(since │ AT │ = │ A │).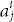 in the determinant
in the determinant 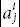 be denoted by
be denoted by 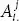 . Then, by summation convention we have
. Then, by summation convention we have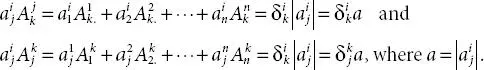
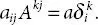
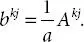
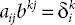
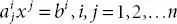
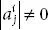
 , where
, where 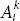 is cofactor of
is cofactor of 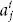 .
.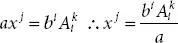 , which is called Cramer’s Rule , for the solution of n linear equations.
, which is called Cramer’s Rule , for the solution of n linear equations.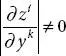 .
.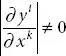 .
.