1 Cover
2 Title Page Matrices and Tensors with Signal Processing Set coordinated by Gérard Favier Volume 2
3 Copyright First published 2021 in Great Britain and the United States by ISTE Ltd and John Wiley & Sons, Inc. Apart from any fair dealing for the purposes of research or private study, or criticism or review, as permitted under the Copyright, Designs and Patents Act 1988, this publication may only be reproduced, stored or transmitted, in any form or by any means, with the prior permission in writing of the publishers, or in the case of reprographic reproduction in accordance with the terms and licenses issued by the CLA. Enquiries concerning reproduction outside these terms should be sent to the publishers at the undermentioned address: ISTE Ltd 27-37 St George’s Road London SW19 4EU UK www.iste.co.uk John Wiley & Sons, Inc. 111 River Street Hoboken, NJ 07030 USA www.wiley.com © ISTE Ltd 2021 The rights of Gérard Favier to be identified as the author of this work have been asserted by him in accordance with the Copyright, Designs and Patents Act 1988. Library of Congress Control Number: 2021938218 British Library Cataloguing-in-Publication Data A CIP record for this book is available from the British Library ISBN 978-1-78630-155-0
4 Introduction
I.1. What are the advantages of tensor approaches? I.2. For what uses? I.3. In what fields of application? I.4. With what tensor decompositions? I.5. With what cost functions and optimization algorithms? I.6. Brief description of content
5 1 Matrix Decompositions1.1. Introduction 1.2. Overview of the most common matrix decompositions 1.3. Eigenvalue decomposition 1.4. URV Hdecomposition 1.5. Singular value decomposition 1.6. CUR decomposition
6 2 Hadamard, Kronecker and Khatri–Rao Products2.1. Introduction 2.2. Notation 2.3. Hadamard product 2.4. Kronecker product 2.5. Kronecker sum 2.6. Index convention 2.7. Commutation matrices 2.8. Relations between the diag operator and the Kronecker product 2.9. Khatri–Rao product 2.10. Relations between vectorization and Kronecker and Khatri–Rao products 2.11. Relations between the Kronecker, Khatri–Rao and Hadamard products 2.12. Applications
7 3 Tensor Operations3.1. Introduction 3.2. Notation and particular sets of tensors 3.3. Notion of slice 3.4. Mode combination 3.5. Partitioned tensors or block tensors 3.6. Diagonal tensors 3.7. Matricization 3.8. Subspaces associated with a tensor and multilinear rank 3.9. Vectorization 3.10. Transposition 3.11. Symmetric/partially symmetric tensors 3.12. Triangular tensors 3.13. Multiplication operations 3.14. Inverse and pseudo-inverse tensors 3.15. Tensor decompositions in the form of factorizations 3.16. Inner product, Frobenius norm and trace of a tensor 3.17. Tensor systems and homogeneous polynomials 3.18. Hadamard and Kronecker products of tensors 3.19. Tensor extension 3.20. Tensorization 3.21. Hankelization
8 4 Eigenvalues and Singular Values of a Tensor4.1. Introduction 4.2. Eigenvalues of a tensor of order greater than two 4.3. Best rank-one approximation 4.4. Orthogonal decompositions 4.5. Singular values of a tensor
9 5 Tensor Decompositions5.1. Introduction 5.2. Tensor models 5.3. Examples of tensor models
10 Appendix Random Variables and Stochastic ProcessesA1.1. Introduction A1.2. Random variables A1.3. Discrete-time random signals A1.4. Application to system identification
11 References
12 Index
13 End User License Agreement
1 Introduction Figure I.1. Third-order PARAFAC model Figure I.2. Third-order Tucker model Figure I.3. Fourth-order TT model
2 Chapter 3Figure 3.1. Fibers of a third-order tensor Figure 3.2. Matrix slices of a third-order tensor Figure 3.3. Unfolding B J1×J2I3.
3 Appendix Random Variables and Stochastic ProcessesFigure A1.1. Symmetry regions of the third-order cumulant
1 Introduction Table I.1. Signal and image tensors Table I.2. Other fields of application Table I.3. Parametric complexity of the CPD, TD, and TT decompositions Table I.4. Cost functions for model estimation and recovery of missing data
2 Chapter 1 Table 1.1. The most common matrix decompositions Table 1.2. Eigenvalues of a real square matrix Table 1.3. Eigenvalues and extrema of the Rayleigh quotient Table 1.4. Eigenvalue properties of certain matrix classes Table 1.5. Eigenvalues of positive/negative (semi-)definite matrices Table 1.6. Equivalent and similar matrices Table 1.7. Fundamental subspaces of A ∈ 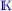 I×J Table 1.8. Relations between the fundamental subspaces Table 1.9. Relations between left and right singular vectors Table 1.10. Definition and properties of the SVD Table 1.11. Relations between the left and right singular vectors Table 1.12. SVD and fundamental subspaces Table 1.13. Computation of an SVD and of the Moore-Penrose pseudo-inverse Table 1.14. Matrix norms Table 1.15. Rank- k approximation and approximation errors Table 1.16. Least squares estimator
I×J Table 1.8. Relations between the fundamental subspaces Table 1.9. Relations between left and right singular vectors Table 1.10. Definition and properties of the SVD Table 1.11. Relations between the left and right singular vectors Table 1.12. SVD and fundamental subspaces Table 1.13. Computation of an SVD and of the Moore-Penrose pseudo-inverse Table 1.14. Matrix norms Table 1.15. Rank- k approximation and approximation errors Table 1.16. Least squares estimator
3 Chapter 2Table 2.1. Hadamard, Kronecker, and Khatri-Rao products and Kronecker sum Table 2.2. Hadamard product of Hermitian positive (semi-)definite matrices Table 2.3. Basic relations satisfied by the Hadamard product Table 2.4. The diag operator and the Hadamard product Table 2.5. Basic relations satisfied by the Kronecker product of vectors Table 2.6. Rank-one matrices and Kronecker products of vectors Table 2.7. Other decompositions of (u ⊗ v)(x ⊗ y) HTable 2.8. Relations involving Kronecker products of vectors Table 2.9. Properties of the multiple Kronecker product Table 2.10. Identities involving matrix-vector Kronecker products Table 2.11. Rank, trace, determinant, and spectrum of a Kronecker product Table 2.12. Kronecker product of positive/negative definite matrices Table 2.13. Structural properties of the Kronecker product Table 2.14. Kronecker products of vectors and index convention Table 2.15. Kronecker products of matrices and index convention Table 2.16. Commutation matrices, vectorization, and Kronecker product Table 2.17. Khatri-Rao product and index convention Table 2.18. Relations between the Hadamard, Khatri-Rao, and Kronecker products Table 2.19. Relations between the Kronecker, Khatri-Rao, and Hadamard products o...Table 2.20. Other relations between the Kronecker, Khatri-Rao, and Hadamard prod...Table 2.21. Basic relations Table 2.22. Vectorization formulae Table 2.23. Partial derivatives of various functions Table 2.24. Derivatives of a scalar function and a vector function Table 2.25. Derivatives of a matrix function with respect to a matrix variable Table 2.26. Definitions of 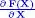 in partitioned form Table 2.27. Other derivatives Table 2.28. Derivatives of matrix traces
in partitioned form Table 2.27. Other derivatives Table 2.28. Derivatives of matrix traces
4 Chapter 3Table 3.1. Notation for sets of indices and dimensions Table 3.2. Various sets of tensors Table 3.3. Multilinear forms and associated tensors Table 3.4. Multilinear forms and associated homogeneous polynomials
Читать дальше

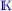 I×J Table 1.8. Relations between the fundamental subspaces Table 1.9. Relations between left and right singular vectors Table 1.10. Definition and properties of the SVD Table 1.11. Relations between the left and right singular vectors Table 1.12. SVD and fundamental subspaces Table 1.13. Computation of an SVD and of the Moore-Penrose pseudo-inverse Table 1.14. Matrix norms Table 1.15. Rank- k approximation and approximation errors Table 1.16. Least squares estimator
I×J Table 1.8. Relations between the fundamental subspaces Table 1.9. Relations between left and right singular vectors Table 1.10. Definition and properties of the SVD Table 1.11. Relations between the left and right singular vectors Table 1.12. SVD and fundamental subspaces Table 1.13. Computation of an SVD and of the Moore-Penrose pseudo-inverse Table 1.14. Matrix norms Table 1.15. Rank- k approximation and approximation errors Table 1.16. Least squares estimator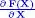 in partitioned form Table 2.27. Other derivatives Table 2.28. Derivatives of matrix traces
in partitioned form Table 2.27. Other derivatives Table 2.28. Derivatives of matrix traces










