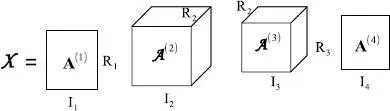
Figure I.3. Fourth-order TT model
– The Tucker decomposition (Tucker 1966) can be viewed as a generalization of the PARAFAC decomposition that takes into account all the interactions between the columns of the matrix factors A(n) ∈ In×Rn via the introduction of a core tensor This decomposition is not unique in general. Note that, if Rn ≤ In for ∀n ∈ 〈N〉, then the core tensor provides a compressed form of χ. If Rn, for n ∈ 〈N〉, is chosen as the rank of the mode-n matrix unfolding6 of χ, then the N-tuple (R1, · · · , RN) is minimal, and it is called the multilinear rank of the tensor.
Such a Tucker decomposition can be obtained using the truncated high-order SVD (THOSVD), under the constraint of column-orthonormal matrices A (n)(de Lathauwer et al . 2000a). This algorithm is described in section 5.2.1.8.
See Figure I.2for a third-order tensor, and Chapter 5for a detailed presentation.
– The TT decomposition (Oseledets 2011) is composed of a train of third-order tensors the first and last carriages of the train being matrices which implies r0 = rN = 1, and therefore The dimensions Rn, for n ∈ 〈N − 1〉, called the TT ranks, are given by the ranks of some matrix unfoldings of the original tensor.
This decomposition has been used to solve the tensor completion problem (Grasedyck et al . 2015; Bengua et al . 2017), for facial recognition (Brandoni and Simoncini 2020) and for modeling MIMO communication channels (Zniyed et al . 2020), among many other applications. A brief description of the TT decomposition is given in section 3.13.4using the mode-( p, n ) product. Note that a specific SVD-based algorithm, called TT-SVD, was proposed by Oseledets (2011) for computing a TT decomposition.
This decomposition and the hierarchical Tucker (HT) one (Grasedyck and Hackbush 2011; Ballani et al . 2013) are special cases of tensor networks (TNs) (Cichocki 2014), as will be discussed in more detail in the next volume.
6 See definition [3.41], in Chapter 3, of the mode- n matrix unfolding X nof a tensor χ , whose columns are the mode- n vectors obtained by fixing all but n indices.
From this brief description of the three tensor models, one can conclude that, unlike matrices, the notion of rank is not unique for tensors, since it depends on the decomposition used. Thus, as mentioned above, one defines the tensor rank (also called the canonical rank or Kruskal’s rank) associated with the PARAFAC decomposition, the multilinear rank that relies on the Tucker’s model, and the TT-ranks linked with the TT decomposition.
It is important to note that the number of characteristic parameters of the PARAFAC and TT decompositions is proportional to N , the order of the tensor, whereas the parametric complexity of the Tucker decomposition increases exponentially with N . This is why the first two decompositions are especially valuable for large-scale problems. Although the Tucker model is not unique in general, imposing an orthogonality constraint on the matrix factors yields the HOSVD decomposition, a truncated form of which gives an approximate solution to the best low multilinear rank approximation problem (de Lathauwer et al . 2000a). This solution, which is based on an a priori choice of the dimensions R nof the core tensor, is to be compared with the truncated SVD in the matrix case, although it does not have the same optimality property. It is widely used to reduce the parametric complexity of data tensors.
From the above, it can be concluded that the TT model combines the advantages of the other two decompositions, in terms of parametric complexity (like PARAFAC) and numerical stability (like Tucker’s model), due to a parameter estimation algorithm based on a calculation of SVDs.
To illustrate the use of the PARAFAC decomposition, let us consider the case of multi-user mobile communications with a CDMA (code-division multiple access) encoding system. The multiple access technique allows multiple emitters to simultaneously transmit information over the same communication channel by assigning a code to each emitter. The information is transmitted as symbols s n,m, with n ∈ 〈 N 〉 and m ∈ 〈 M 〉, where N and M are the number of transmission time slots, i.e. the number of symbol periods, and the number of emitting antennas, respectively. The symbols belong to a finite alphabet that depends on the modulation being used. They are encoded with a space-time coding that introduces code diversity by repeating each symbol P times with a code c p,massigned to the m th emitting antenna, p ∈ 〈 P 〉, where P denotes the length of the spreading code. The signal received by the k th receiving antenna, during the n th symbol period and the p th chip period, is a linear combination of the symbols encoded and transmitted by the M emitting antennas:
[I.1] 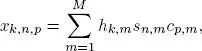
where h k,mis the fading coefficient of the communication channel between the receiving antenna k and the emitting antenna m .
The received signals, which are complex-valued, therefore form a third-order tensor 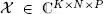 whose modes are: space × time × code , associated with the indices ( k, n, p ). This signal tensor satisfies a PARAFAC decomposition [[ H, S, C; M ]] whose rank is equal to the number M of emitting antennas and whose matrix factors are the channel
whose modes are: space × time × code , associated with the indices ( k, n, p ). This signal tensor satisfies a PARAFAC decomposition [[ H, S, C; M ]] whose rank is equal to the number M of emitting antennas and whose matrix factors are the channel 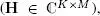 the matrix of transmitted symbols
the matrix of transmitted symbols  This example is a simplified form of the DS-CDMA (direct-sequence CDMA) system proposed by (Sidiropoulos et al . 2000b).
This example is a simplified form of the DS-CDMA (direct-sequence CDMA) system proposed by (Sidiropoulos et al . 2000b).
I.5. With what cost functions and optimization algorithms?
We will now briefly describe the most common processing operations carried out with tensors, as well as some of the optimization algorithms that are used. It is important to first present the preprocessing operations that need to be performed. Preprocessing typically involves data centering operations (offset elimination), scaling of non-homogeneous data, suppression of outliers and artifacts, image adjustment (size, brightness, contrast, alignment, etc.), denoising, signal transformation using certain transforms (wavelets, Fourier, etc.), and finally, in some cases, the calculation of statistics of signals to be processed.
Preprocessing is fundamental, both to improve the quality of the estimated models and, therefore, of the subsequent processing operations, and to avoid numerical problems with optimization algorithms, such as conditioning problems that may cause the algorithms to fail to converge. Centering and scaling preprocessing operations are potentially problematic because they are interdependent and can be combined in several different ways. If data are missing, centering can also reduce the rank of the tensor model. For a more detailed description of these preprocessing operations, see Smilde et al . (2004).
Читать дальше


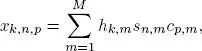
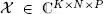 whose modes are: space × time × code , associated with the indices ( k, n, p ). This signal tensor satisfies a PARAFAC decomposition [[ H, S, C; M ]] whose rank is equal to the number M of emitting antennas and whose matrix factors are the channel
whose modes are: space × time × code , associated with the indices ( k, n, p ). This signal tensor satisfies a PARAFAC decomposition [[ H, S, C; M ]] whose rank is equal to the number M of emitting antennas and whose matrix factors are the channel 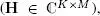 the matrix of transmitted symbols
the matrix of transmitted symbols  This example is a simplified form of the DS-CDMA (direct-sequence CDMA) system proposed by (Sidiropoulos et al . 2000b).
This example is a simplified form of the DS-CDMA (direct-sequence CDMA) system proposed by (Sidiropoulos et al . 2000b).










