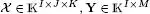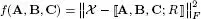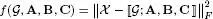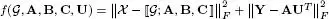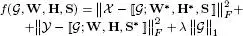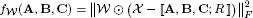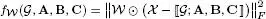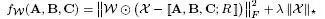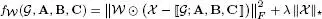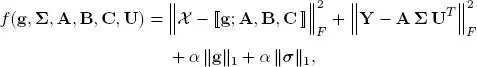For the processing operations themselves, we can distinguish between several different classes:
– supervised/non-supervised (blind or semi-blind), i.e. with or without training data, for example, to solve classification problems, or when a priori information, called a pilot sequence, is transmitted to the receiver for channel estimation;
– real-time (online)/batch (offline) processing;
– centralized/distributed;
– adaptive/blockwise (with respect to the data);
– with/without coupling of tensor and/or matrix models;
– with/without missing data.
It is important to distinguish batch processing, which is performed to analyze data recorded as signal and image sets, from the real-time processing required by wireless communication systems, recommendation systems, web searches and social networks. In real-time applications, the dimensionality of the model and the algorithmic complexity are predominant factors. The signals received by receiving antennas, the information exchanged between a website and the users and the messages exchanged between the users of a social network are time-dependent. For instance, a recommendation system interacts with the users in real-time, via a possible extension of an existing database by means of machine learning techniques. For a description of various applications of tensors for data mining and machine learning, see Anandkumar et al . (2014) and Sidiropoulos et al . (2017).
Tensor-based processings lead to various types of optimization algorithm as follows:
– constrained/unconstrained optimization;
– iterative/non-iterative, or closed-form;
– alternating/global;
– sequential/parallel.
Furthermore, depending on the information that is available a priori , different types of constraints can be taken into account in the cost function to be optimized: low rank, sparseness, non-negativity, orthogonality and differentiability/smoothness. In the case of constrained optimization, weights need to be chosen in the cost function according to the relative importance of each constraint and the quality of the a priori information that is available.
Table I.4presents a few examples of cost functions that can be minimized for the parameter estimation of certain third-order tensor models (CPD, Tucker, coupled matrix Tucker (CMTucker) and coupled sparse tensor factorization (CSTF)), for the imputation of missing data in a tensor and for the estimation of a sparse data tensor with a low-rank constraint expressed in the form of the nuclear norm of the tensor.
REMARK I.1.– We can make the following remarks:
– the cost functions presented in Table I.4correspond to data fitting criteria. These criteria, expressed in terms of tensor and matrix Frobenius norms (||.||F), are quadratic in the difference between the data tensor χ and the output of CPD and TD models, as well as between the data matrix Y and a matrix factorization model, in the case of the CMTucker model. They are trilinear and quadrilinear, respectively, with respect to the parameters of the CPD and TD models to be estimated, and bilinear with respect to the parameters of the matrix factorization model;
– for the missing data imputation problem using a CPD or TD model, the binary tensor , which has the same size as χ, is defined as:
[I.2] 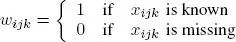
The purpose of the Hadamard product (denoted  ) of
) of 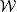 , with the difference between χ and the output of the CPD and TD models, is to fit the model to the available data only, ignoring any missing data for model estimation. This imputation problem, known as the tensor completion problem, was originally dealt with by Tomasi and Bro (2005) and Acar et al . (2011a) using a CPD model, followed by Filipovic and Jukic (2015) using a TD model. Various articles have discussed this problem in the context of different applications. An overview of the literature will be given in the next volume;
, with the difference between χ and the output of the CPD and TD models, is to fit the model to the available data only, ignoring any missing data for model estimation. This imputation problem, known as the tensor completion problem, was originally dealt with by Tomasi and Bro (2005) and Acar et al . (2011a) using a CPD model, followed by Filipovic and Jukic (2015) using a TD model. Various articles have discussed this problem in the context of different applications. An overview of the literature will be given in the next volume;
Table I.4. Cost functions for model estimation and recovery of missing data
| ProblemsData |
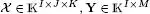 |
| Estimation |
Cost functions |
| CPD |
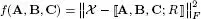 |
| TD |
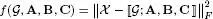 |
| CMTucker |
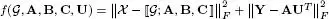 |
| CSTF |
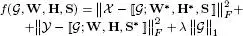 |
| Imputation |
Cost functions |
| CPD |
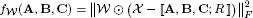 |
| TD |
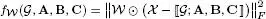 |
| Imputation with low-rank constraint |
Cost functions |
| CPD |
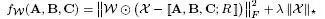 |
| TD |
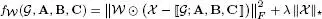 |
– for the imputation problem with the low-rank constraint, the term χ in the cost function replaces the low-rank constraint with the nuclear norm of χ, since the function rank (χ) is not convex, and the nuclear norm is the closest convex approximation of the rank. In Liu et al. (2013), this term is replaced by where Xn represents the mode-n unfolding of χ7;
– in the case of the CMTucker model, the coupling considered here relates to the first modes of the tensor χ and the matrix Y of data via the common matrix factor A.
Coupled matrix and tensor factorization (CMTF) models were introduced in Acar et al . (2011b) by coupling a CPD model with a matrix factorization and using the gradient descent algorithm to estimate the parameters. This type of model was used by Acar et al . (2017) to merge EEG and fMRI data with the goal of analyzing brain activity. The EEG signals are modeled with a normalized CPD model (see Chapter 5), whereas the fMRI data are modeled with a matrix factorization. The data are coupled through the subjects mode (see Table I.1). The cost function to be minimized is therefore given by:
[I.3] 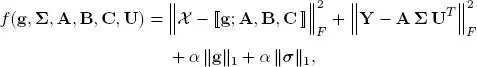
Читать дальше

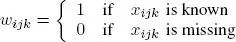
 ) of
) of 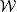 , with the difference between χ and the output of the CPD and TD models, is to fit the model to the available data only, ignoring any missing data for model estimation. This imputation problem, known as the tensor completion problem, was originally dealt with by Tomasi and Bro (2005) and Acar et al . (2011a) using a CPD model, followed by Filipovic and Jukic (2015) using a TD model. Various articles have discussed this problem in the context of different applications. An overview of the literature will be given in the next volume;
, with the difference between χ and the output of the CPD and TD models, is to fit the model to the available data only, ignoring any missing data for model estimation. This imputation problem, known as the tensor completion problem, was originally dealt with by Tomasi and Bro (2005) and Acar et al . (2011a) using a CPD model, followed by Filipovic and Jukic (2015) using a TD model. Various articles have discussed this problem in the context of different applications. An overview of the literature will be given in the next volume;