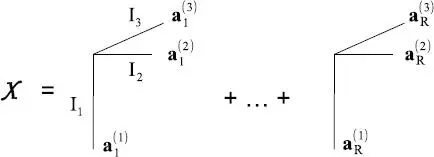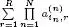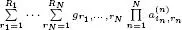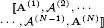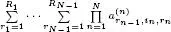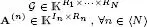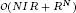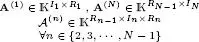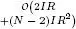The articles by Bobadilla et al . (2013) and Frolov and Oseledets (2017) present various recommendation systems with many bibliographical references. Operating according to a similar principle as recommendation systems, social network websites, such as Wikipedia, Facebook, or Twitter, allow different types of data to be exchanged and shared, content to be produced and connections to be established.
I.4. With what tensor decompositions?
It is important to note that, for an N th-order tensor 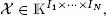 the number of elements is
the number of elements is 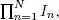 and, assuming I n = I for n ∈ 〈 N 〉, this number becomes I N , which induces an exponential increase with the tensor order N . This is called the curse of dimensionality (Oseledets and Tyrtyshnikov 2009). For big data tensors, tensor decompositions play a fundamental role in alleviating this curse of dimensionality, due to the fact that the number of parameters that characterize the decompositions is generally much smaller than the number of elements in the original tensor.
and, assuming I n = I for n ∈ 〈 N 〉, this number becomes I N , which induces an exponential increase with the tensor order N . This is called the curse of dimensionality (Oseledets and Tyrtyshnikov 2009). For big data tensors, tensor decompositions play a fundamental role in alleviating this curse of dimensionality, due to the fact that the number of parameters that characterize the decompositions is generally much smaller than the number of elements in the original tensor.
We now introduce three basic decompositions: PARAFAC/CANDECOMP/CPD, TD and TT 5. The first two are studied in depth in Chapter 5, whereas the third, briefly introduced in Chapter 3, will be considered in more detail in Volume 3.
Table I.3gives the expression of the element 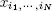 of a tensor
of a tensor 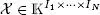 of order N and size I 1× · • · × I N, either real (
of order N and size I 1× · • · × I N, either real ( 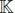 = ℝ) or complex (
= ℝ) or complex ( 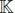 = ℂ), for each of the three decompositions cited above. Their parametric complexity is compared in terms of the size of each matrix and tensor factor, assuming I n= I and R n= R for all n ∈ 〈 N 〉.
= ℂ), for each of the three decompositions cited above. Their parametric complexity is compared in terms of the size of each matrix and tensor factor, assuming I n= I and R n= R for all n ∈ 〈 N 〉.
Figures I.1– I.3show graphical representations of the PARAFAC model 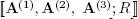 and the TD model
and the TD model 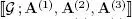 for a third-order tensor
for a third-order tensor 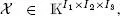 and of the TT model [[ A (1),
and of the TT model [[ A (1),  (2),
(2),  (3), A (4)]] for a fourth-order tensor χ ∈
(3), A (4)]] for a fourth-order tensor χ ∈ 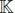 I1×I2×I3×I4. In the case of the PARAFAC model, we define
I1×I2×I3×I4. In the case of the PARAFAC model, we define 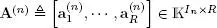 using its columns, for n ∈ {1, 2, 3}.
using its columns, for n ∈ {1, 2, 3}.
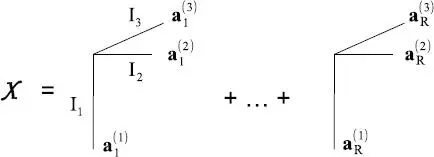
Figure I.1. Third-order PARAFAC model
We can make a few remarks about each of these decompositions:
– The PARAFAC decomposition (Harshman 1970), also known as CANDECOMP (Carroll and Chang 1970) or CPD (Hitchcock 1927), of a Nth-order tensor χ is a sum of R rank-one tensors, each defined as the outer product of one column from each of the N matrix factors A(n) ∈ In×R. When R is minimal, it is called the rank of the tensor. If the matrix factors satisfy certain conditions, this decomposition has the essential uniqueness property. See Figure I.1for a third-order tensor (N = 3), and Chapter 5for a detailed presentation.
Table I.3. Parametric complexity of the CPD, TD, and TT decompositions
| Decompositions |
Notation |
Element x i1,···, iN |
| PARAFAC / CPD |
[[ A (1), · · · , A (N); R ]] |
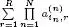 |
| TD |
 |
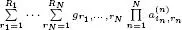 |
| TT |
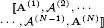 |
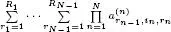 |
| Decompositions |
Parameters |
Complexity |
| CPD |
A (n)∈ 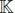 In×R, ∀ n ∈ 〈 N 〉 In×R, ∀ n ∈ 〈 N 〉 |
O( N I R ) |
| TD |
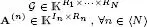 |
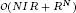 |
| TT |
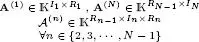 |
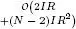 |
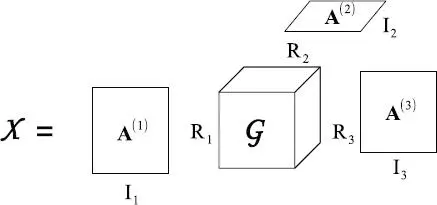
Figure I.2. Third-order Tucker model
Читать дальше

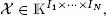 the number of elements is
the number of elements is 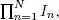 and, assuming I n = I for n ∈ 〈 N 〉, this number becomes I N , which induces an exponential increase with the tensor order N . This is called the curse of dimensionality (Oseledets and Tyrtyshnikov 2009). For big data tensors, tensor decompositions play a fundamental role in alleviating this curse of dimensionality, due to the fact that the number of parameters that characterize the decompositions is generally much smaller than the number of elements in the original tensor.
and, assuming I n = I for n ∈ 〈 N 〉, this number becomes I N , which induces an exponential increase with the tensor order N . This is called the curse of dimensionality (Oseledets and Tyrtyshnikov 2009). For big data tensors, tensor decompositions play a fundamental role in alleviating this curse of dimensionality, due to the fact that the number of parameters that characterize the decompositions is generally much smaller than the number of elements in the original tensor.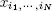 of a tensor
of a tensor 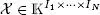 of order N and size I 1× · • · × I N, either real (
of order N and size I 1× · • · × I N, either real ( 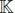 = ℝ) or complex (
= ℝ) or complex ( 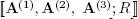 and the TD model
and the TD model 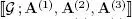 for a third-order tensor
for a third-order tensor 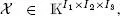 and of the TT model [[ A (1),
and of the TT model [[ A (1),  (2),
(2), 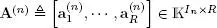 using its columns, for n ∈ {1, 2, 3}.
using its columns, for n ∈ {1, 2, 3}.