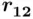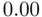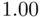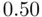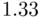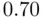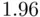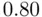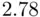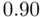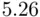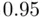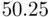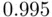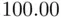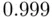Samprit Chatterjee - Handbook of Regression Analysis With Applications in R
Здесь есть возможность читать онлайн «Samprit Chatterjee - Handbook of Regression Analysis With Applications in R» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Handbook of Regression Analysis With Applications in R
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:3 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Handbook of Regression Analysis With Applications in R: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Handbook of Regression Analysis With Applications in R»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
andbook and reference guide for students and practitioners of statistical regression-based analyses in R
Handbook of Regression Analysis
with Applications in R, Second Edition
The book further pays particular attention to methods that have become prominent in the last few decades as increasingly large data sets have made new techniques and applications possible. These include:
Regularization methods Smoothing methods Tree-based methods In the new edition of the
, the data analyst’s toolkit is explored and expanded. Examples are drawn from a wide variety of real-life applications and data sets. All the utilized R code and data are available via an author-maintained website.
Of interest to undergraduate and graduate students taking courses in statistics and regression, the
will also be invaluable to practicing data scientists and statisticians.

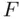 ‐statistic to test the overall significance of the regression is a special case of this construction (with restriction
‐statistic to test the overall significance of the regression is a special case of this construction (with restriction 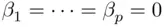 ), as is each of the individual
), as is each of the individual 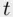 ‐statistics that test the significance of any variable (with restriction
‐statistics that test the significance of any variable (with restriction 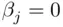 ). In the latter case
). In the latter case 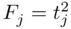 .
. ‐tests when predictors are correlated with each other. A related issue is that of collinearity(sometimes somewhat redundantly referred to as multicollinearity), which refers to the situation when (some of) the predictors are highly correlated with each other. The presence of predicting variables that are highly correlated with each other can lead to instability in the regression coefficients, increasing their standard errors, and as a result the
‐tests when predictors are correlated with each other. A related issue is that of collinearity(sometimes somewhat redundantly referred to as multicollinearity), which refers to the situation when (some of) the predictors are highly correlated with each other. The presence of predicting variables that are highly correlated with each other can lead to instability in the regression coefficients, increasing their standard errors, and as a result the  ‐statistics for the variables can be deflated. This can be seen in Figure 2.1. The two plots refer to identical data sets, other than the one data point that is lightly colored. Dropping the data points down to the
‐statistics for the variables can be deflated. This can be seen in Figure 2.1. The two plots refer to identical data sets, other than the one data point that is lightly colored. Dropping the data points down to the 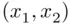 plane makes clear the high correlation between the predictors. The estimated regression plane changes from
plane makes clear the high correlation between the predictors. The estimated regression plane changes from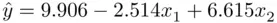
 ‐statistic is significant, yet each of the individual
‐statistic is significant, yet each of the individual 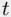 ‐statistics is not significant (more generally, the tail probability for the
‐statistics is not significant (more generally, the tail probability for the 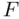 ‐test is considerably smaller than those of any of the individual coefficient
‐test is considerably smaller than those of any of the individual coefficient 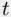 ‐tests). Second, if the data are changed only slightly, the fitted regression coefficients can change dramatically. Note that while collinearity can have a large effect on regression coefficients and associated
‐tests). Second, if the data are changed only slightly, the fitted regression coefficients can change dramatically. Note that while collinearity can have a large effect on regression coefficients and associated 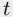 ‐statistics, it does not have a large effect on overall measures of fit like the overall
‐statistics, it does not have a large effect on overall measures of fit like the overall 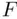 ‐test or
‐test or  , since adding unneeded variables (whether or not they are collinear with predictors already in the model) cannot increase the residual sum of squares (it can only decrease it or leave it roughly the same).
, since adding unneeded variables (whether or not they are collinear with predictors already in the model) cannot increase the residual sum of squares (it can only decrease it or leave it roughly the same).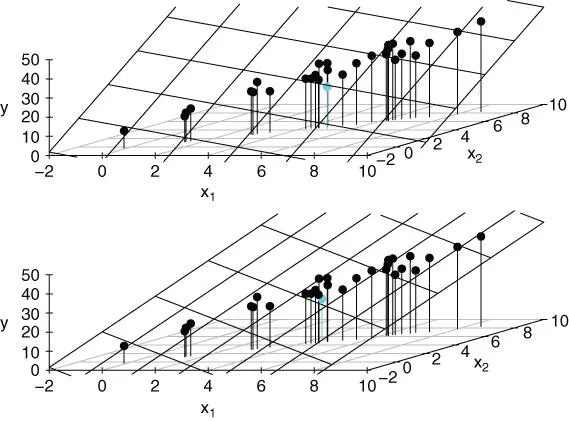
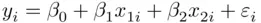
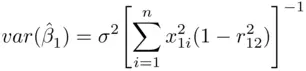
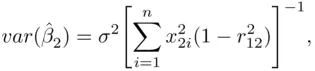
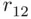 is the correlation between
is the correlation between  and
and 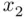 . Note that as collinearity increases (
. Note that as collinearity increases ( 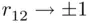 ), both variances tend to
), both variances tend to 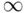 . This effect is quantified in Table 2.1.
. This effect is quantified in Table 2.1.