Since all of these methods depend on the assumptions holding, a fundamental part of any regression analysis is to check those assumptions. The residual plots discussed in this chapter are a key part of that process, and other diagnostics and tests will be discussed in future chapters that provide additional support for that task.
AutocorrelationCorrelation between adjacent observations in a (time) series. In the regression context it is autocorrelation of the errors that is a violation of assumptions. Coefficient of determination ( 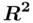 )The square of the multiple correlation coefficient, estimates the proportion of variability in the target variable that is explained by the predictors in the linear model. Confidence interval for a fitted valueA measure of precision of the estimate of the expected target value for a given
)The square of the multiple correlation coefficient, estimates the proportion of variability in the target variable that is explained by the predictors in the linear model. Confidence interval for a fitted valueA measure of precision of the estimate of the expected target value for a given 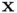 . Dependent variableCharacteristic of each member of the sample that is being modeled. This is also known as the targetor responsevariable. Fitted valueThe least squares estimate of the expected target value for a particular observation obtained from the fitted regression model. HeteroscedasticityUnequal variance; this can refer to observed unequal variance of the residuals or theoretical unequal variance of the errors. HomoscedasticityEqual variance; this can refer to observed equal variance of the residuals or the assumed equal variance of the errors. Independent variable(s)Characteristic(s) of each member of the sample that could be used to model the dependent variable. These are also known as the predictingvariables. Least squaresA method of estimation that minimizes the sum of squared deviations of the observed target values from their estimated expected values. Prediction intervalThe interval estimate for the value of the target variable for an individual member of the population using the fitted regression model. ResidualThe difference between the observed target value and the corresponding fitted value. Residual mean squareAn unbiased estimate of the variance of the errors. It is obtained by dividing the sum of squares of the residuals by
. Dependent variableCharacteristic of each member of the sample that is being modeled. This is also known as the targetor responsevariable. Fitted valueThe least squares estimate of the expected target value for a particular observation obtained from the fitted regression model. HeteroscedasticityUnequal variance; this can refer to observed unequal variance of the residuals or theoretical unequal variance of the errors. HomoscedasticityEqual variance; this can refer to observed equal variance of the residuals or the assumed equal variance of the errors. Independent variable(s)Characteristic(s) of each member of the sample that could be used to model the dependent variable. These are also known as the predictingvariables. Least squaresA method of estimation that minimizes the sum of squared deviations of the observed target values from their estimated expected values. Prediction intervalThe interval estimate for the value of the target variable for an individual member of the population using the fitted regression model. ResidualThe difference between the observed target value and the corresponding fitted value. Residual mean squareAn unbiased estimate of the variance of the errors. It is obtained by dividing the sum of squares of the residuals by 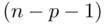 , where
, where 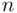 is the number of observations and
is the number of observations and 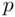 is the number of predicting variables. Standard error of the estimate (
is the number of predicting variables. Standard error of the estimate ( 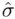 )An estimate of
)An estimate of  , the standard deviation of the errors, equaling the square root of the residual mean square.
, the standard deviation of the errors, equaling the square root of the residual mean square.
CHAPTER TWO Model Building
1 2.1 Introduction
2 2.2 Concepts and Background Material 2.2.1Using Hypothesis Tests to Compare Models 2.2.2Collinearity
3 2.3 Methodology 2.3.1Model Selection 2.3.2Example—Estimating Home Prices (continued)
4 2.4 Indicator Variables and Modeling Interactions 2.4.1Example—Electronic Voting and the 2004 Presidential Election
5 2.5 Summary
All of the discussion in Chapter 1is based on the premise that the only model being considered is the one currently being fit. This is not a good data analysis strategy, for several reasons.
1 Including unnecessary predictors in the model (what is sometimes called overfitting) complicates descriptions of the process. Using such models tends to lead to poorer predictions because of the additional unnecessary noise. Further, a more complex representation of the true regression relationship is less likely to remain stable enough to be useful for future prediction than is a simpler one.
2 Omitting important effects (underfitting) reduces predictive power, biases estimates of effects for included predictors, and results in less understanding of the process being studied.
3 Violations of assumptions should be addressed, so that least squares estimation is justified.
The last of these reasons is the subject of later chapters, while the first two are discussed in this chapter. This operation of choosing among different candidate models so as to avoid overfitting and underfitting is called model selection.
First, we discuss the uses of hypothesis testing for model selection. Various hypothesis tests address relevant model selection questions, but there are also reasons why they are not sufficient for these purposes. Part of these difficulties is the effect of correlations among the predictors, and the situation of high correlation among the predictors ( collinearity) is a particularly challenging one.
A useful way of thinking about the tradeoffs of overfitting versus underfitting is as a contrast between strength of fit and simplicity. The principle of parsimonystates that a model should be as simple as possible while still accounting for the important relationships in the data. Thus, a sensible way of comparing models is using measures that explicitly reflect this tradeoff; such measures are discussed in Section 2.3.1.
The chapter concludes with a discussion of techniques designed to address the existence of well‐defined subgroups in the data. In this situation, it is often the case that the effects of a predictor on the target variable is different in the two groups, and ways of building models to handle this are discussed in Section 2.4.
2.2 Concepts and Background Material
2.2.1 USING HYPOTHESIS TESTS TO COMPARE MODELS
Determining whether individual regression coefficients are statistically significant (as discussed in Section 1.3.3) is an obvious first step in deciding whether a model is overspecified. A predictor that does not add significantly to model fit should have an estimated slope coefficient that is not significantly different from 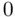 , and is thus identified by a small
, and is thus identified by a small 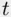 ‐statistic. So, for example, in the analysis of home prices in Section 1.4, the regression output on page 17 suggests removing number of bedrooms, lot size, and property taxes from the model, as all three have insignificant
‐statistic. So, for example, in the analysis of home prices in Section 1.4, the regression output on page 17 suggests removing number of bedrooms, lot size, and property taxes from the model, as all three have insignificant  ‐values.
‐values.
Recall that 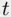 ‐tests can only assess the contribution of a predictor given all of the others in the model. When predictors are correlated with each other,
‐tests can only assess the contribution of a predictor given all of the others in the model. When predictors are correlated with each other, 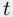 ‐tests can give misleading indications of the importance of a predictor. Consider a two‐predictor situation where the predictors are each highly correlated with the target variable, and are also highly correlated with each other. In this situation, it is likely that the
‐tests can give misleading indications of the importance of a predictor. Consider a two‐predictor situation where the predictors are each highly correlated with the target variable, and are also highly correlated with each other. In this situation, it is likely that the 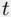 ‐statistic for each predictor will be relatively small. This is not an inappropriate result, since given one predictor the other adds little (being highly correlated with each other, one is redundant in the presence of the other). This means that the
‐statistic for each predictor will be relatively small. This is not an inappropriate result, since given one predictor the other adds little (being highly correlated with each other, one is redundant in the presence of the other). This means that the 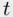 ‐statistics are not effective in identifying important predictors when the two variables are highly correlated.
‐statistics are not effective in identifying important predictors when the two variables are highly correlated.
Читать дальше

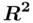 )The square of the multiple correlation coefficient, estimates the proportion of variability in the target variable that is explained by the predictors in the linear model. Confidence interval for a fitted valueA measure of precision of the estimate of the expected target value for a given
)The square of the multiple correlation coefficient, estimates the proportion of variability in the target variable that is explained by the predictors in the linear model. Confidence interval for a fitted valueA measure of precision of the estimate of the expected target value for a given 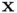 . Dependent variableCharacteristic of each member of the sample that is being modeled. This is also known as the targetor responsevariable. Fitted valueThe least squares estimate of the expected target value for a particular observation obtained from the fitted regression model. HeteroscedasticityUnequal variance; this can refer to observed unequal variance of the residuals or theoretical unequal variance of the errors. HomoscedasticityEqual variance; this can refer to observed equal variance of the residuals or the assumed equal variance of the errors. Independent variable(s)Characteristic(s) of each member of the sample that could be used to model the dependent variable. These are also known as the predictingvariables. Least squaresA method of estimation that minimizes the sum of squared deviations of the observed target values from their estimated expected values. Prediction intervalThe interval estimate for the value of the target variable for an individual member of the population using the fitted regression model. ResidualThe difference between the observed target value and the corresponding fitted value. Residual mean squareAn unbiased estimate of the variance of the errors. It is obtained by dividing the sum of squares of the residuals by
. Dependent variableCharacteristic of each member of the sample that is being modeled. This is also known as the targetor responsevariable. Fitted valueThe least squares estimate of the expected target value for a particular observation obtained from the fitted regression model. HeteroscedasticityUnequal variance; this can refer to observed unequal variance of the residuals or theoretical unequal variance of the errors. HomoscedasticityEqual variance; this can refer to observed equal variance of the residuals or the assumed equal variance of the errors. Independent variable(s)Characteristic(s) of each member of the sample that could be used to model the dependent variable. These are also known as the predictingvariables. Least squaresA method of estimation that minimizes the sum of squared deviations of the observed target values from their estimated expected values. Prediction intervalThe interval estimate for the value of the target variable for an individual member of the population using the fitted regression model. ResidualThe difference between the observed target value and the corresponding fitted value. Residual mean squareAn unbiased estimate of the variance of the errors. It is obtained by dividing the sum of squares of the residuals by 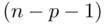 , where
, where 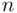 is the number of observations and
is the number of observations and 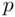 is the number of predicting variables. Standard error of the estimate (
is the number of predicting variables. Standard error of the estimate ( 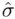 )An estimate of
)An estimate of  , the standard deviation of the errors, equaling the square root of the residual mean square.
, the standard deviation of the errors, equaling the square root of the residual mean square.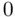 , and is thus identified by a small
, and is thus identified by a small 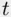 ‐statistic. So, for example, in the analysis of home prices in Section 1.4, the regression output on page 17 suggests removing number of bedrooms, lot size, and property taxes from the model, as all three have insignificant
‐statistic. So, for example, in the analysis of home prices in Section 1.4, the regression output on page 17 suggests removing number of bedrooms, lot size, and property taxes from the model, as all three have insignificant  ‐values.
‐values.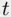 ‐tests can only assess the contribution of a predictor given all of the others in the model. When predictors are correlated with each other,
‐tests can only assess the contribution of a predictor given all of the others in the model. When predictors are correlated with each other, 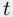 ‐tests can give misleading indications of the importance of a predictor. Consider a two‐predictor situation where the predictors are each highly correlated with the target variable, and are also highly correlated with each other. In this situation, it is likely that the
‐tests can give misleading indications of the importance of a predictor. Consider a two‐predictor situation where the predictors are each highly correlated with the target variable, and are also highly correlated with each other. In this situation, it is likely that the 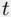 ‐statistic for each predictor will be relatively small. This is not an inappropriate result, since given one predictor the other adds little (being highly correlated with each other, one is redundant in the presence of the other). This means that the
‐statistic for each predictor will be relatively small. This is not an inappropriate result, since given one predictor the other adds little (being highly correlated with each other, one is redundant in the presence of the other). This means that the 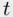 ‐statistics are not effective in identifying important predictors when the two variables are highly correlated.
‐statistics are not effective in identifying important predictors when the two variables are highly correlated.










