Samprit Chatterjee - Handbook of Regression Analysis With Applications in R

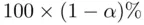As is always the case, a confidence interval provides an alternative way of summarizing the degree of precision in the estimate of a regression parameter. A confidence interval for 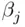has the form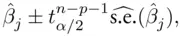

where is the appropriate critical value at two‐sided level 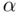for a 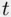‐distribution on 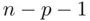degrees of freedom.

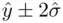The rough prediction interval discussed in Section 1.3.2is an approximate 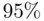interval because it ignores the variability caused by the need to estimate 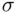and uses only an approximate normal‐based critical value. A more accurate assessment of predictive power is provided by a prediction intervalgiven a particular value of 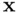. This interval provides guidance as to how precise 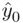is as a prediction of 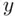for some particular specified value 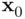, where 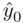is determined by substituting the values 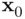into the estimated regression equation. Its width depends on both 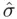and the position of 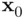relative to the centroid of the predictors (the point located at the means of all predictors), since values farther from the centroid are harder to predict as precisely. Specifically, for a simple regression, the estimated standard error of a predicted value based on a value 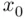of the predicting variable is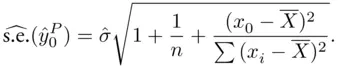

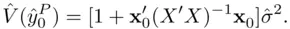
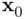More generally, the variance of a predicted value is

(1.10)

Here is taken to include a 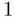in the first entry (corresponding to the intercept in the regression model). The prediction interval is then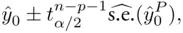

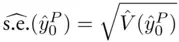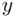where .

This prediction interval should not be confused with a confidence interval for a fitted value. The prediction interval is used to provide an interval estimate for a prediction of for one member of the population with a particular value of 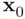; the confidence interval is used to provide an interval estimate for the true expected value of 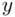for all members of the population with a particular value of 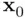. The corresponding standard error, termed the standard error for a fitted value, is the square root of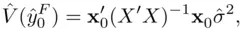

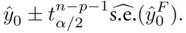
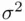(1.11)

with corresponding confidence interval

A comparison of the two estimated variances (1.10)and (1.11)shows that the variance of the predicted value has an extra term, which corresponds to the inherent variability in the population. Thus, the confidence interval for a fitted value will always be narrower than the prediction interval, and is often much narrower (especially for large samples), since increasing the sample size will always improve estimation of the expected response value, but cannot lessen the inherent variability in the population associated with the prediction of the target for a single observation.