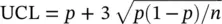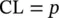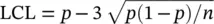As v increases, the Student's t ‐distribution tends to a normal (0, 1) distribution.
Yet another important probability distribution commonly used in the literature of the control charts for non‐normal random variables is the Gamma distribution. The probability distribution of the Gamma distribution can be defined as
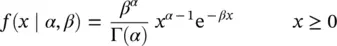
with the scale parameter β > 0 and the shape parameter α > 0.
The mean and variance of the Gamma distribution are
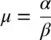
and
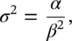
respectively (Montgomery, 2009).
Discrete Probability Distributions
Binomial Probability Distribution
Let a process consists of a set of n independent trials. Here the term independent means that any outcome is not affected by the previous outcome whether it had occurred or not. Here we define any outcome as either success or failure. Suppose that the probability of success is denoted by p , p belongs to the interval (0,1), and the probability of failure is denoted by q = 1 − p , then the binomial probability distribution can be defined as
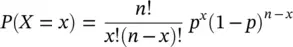
where n is the total number of independent trials and x is a binomial random variable ranging from 0 to n . This distribution has only two parameters n and p . The distribution is symmetric when 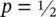 , the distribution is positively skewed if
, the distribution is positively skewed if 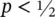 , and it is negatively skewed if
, and it is negatively skewed if 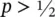 .
.
The binomial probability distribution is the most commonly used distribution in the control chart literature to model the number cases in a sample of n items when the proportion in the population is known. For example, if the proportion of defective item in any mass production unit is 0.12, then find the complete binomial probability distribution for n = 10 ( Table 1.1).
Poisson Probability Distribution
The Poisson distribution is another important discrete probability distribution used for calculating the characteristics of the control chart, which identifies a given number of defects per unit; for instance, the number of stones in a piece of glass of the given size or the number of defects in the manufacturing of items, etc. This distribution has only one parameter μ .
Table 1.1 Probabilities of number of defective items using binomial distribution.
| No. of defective items |
Probability |
No. of defective items |
Probability |
| 0 |
0.27850098 |
6 |
0.00037604 |
| 1 |
0.37977406 |
7 |
0.00002930 |
| 2 |
0.23304317 |
8 |
0.00000150 |
| 3 |
0.08474297 |
9 |
0.00000005 |
| 4 |
0.02022275 |
10 |
0.00000000 |
| 5 |
0.00330918 |
Total |
1.00000000 |
The mean and standard deviation of the binomial distribution are np = 1.2 and 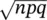 = 1.264911, respectively.
= 1.264911, respectively.
Table 1.2 Probabilities of number of defective items using Poisson distribution.
| No. of defective items |
Probability |
No. of defective items |
Probability |
| 0 |
0.110803158 |
6 |
0.017448405 |
| 1 |
0.243766948 |
7 |
0.005483784 |
| 2 |
0.268143643 |
8 |
0.001508041 |
| 3 |
0.196638672 |
9 |
0.000368632 |
| 4 |
0.108151269 |
10 |
0.000081099 |
| 5 |
0.047586559 |
11 and more |
0.000019789 |
The mean and standard deviation of this distribution are μ = 2.5 and 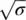 = 1.58, respectively.
= 1.58, respectively.
The frequency distribution of the Poisson distribution can be defined as
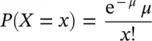
where μ = mean number of defects, μ > 0, e = 2.71828… and x = number of occurrences, x = 0, 1, 2, 3, …
Suppose that the average number of stones in a glass of a particular shape was 2.5. Find the probabilities of different number of stones in the glass. Evaluating the Poisson distribution in this case, we get the results shown in Table 1.2.
1.5 Types of Control Charts
Broadly speaking, there are two types of control charts, i.e. attribute control charts and variable control charts.
1.5.1 Attribute Control Charts
When articles or units are studied on the basis of qualitative measures as go/no go, yes/no, satisfied/not satisfied, positive/negative, etc., then an attribute control chart is suitable to monitor the unusual changes. These are the charts commonly known as p ‐chart used for monitoring proportion of nonconforming items in a sample or proportion of defective items in a sample, and np ‐chart is used to monitor the number of nonconforming items in a sample of size n .
The control limits of these control charts are similar particularly when the sample size is fixed. The limits of p ‐chart charts may be constructed by using the binomial probability distribution with parameter p . As we know that the mean of the binomial distribution is np and its standard deviation is 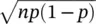 . Thus
. Thus
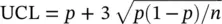
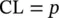
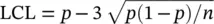
And the control limits for the np ‐chart can be constructed as
Читать дальше

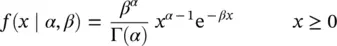
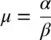
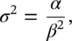
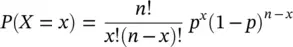
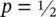 , the distribution is positively skewed if
, the distribution is positively skewed if 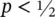 , and it is negatively skewed if
, and it is negatively skewed if 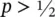 .
.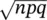 = 1.264911, respectively.
= 1.264911, respectively.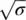 = 1.58, respectively.
= 1.58, respectively.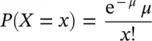
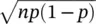 . Thus
. Thus