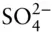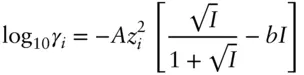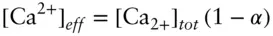Table 3.2b Debye–Hückel effective radii.
| Ion |
å (10 –8cm) |
Rb +, Cs +, 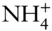 , Ag + , Ag + |
2.5 |
K +, Cl –, Br –, I –, 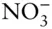 |
3 |
OH –, F –, HS –, 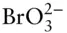 , , 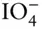 , , 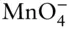 |
3.5 |
Na +, 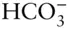 , , 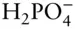 , , 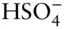 , , 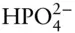 , , 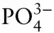 |
4.0–4.5 |
Pb 2+, 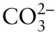 , , 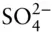 |
4.5 |
| Sr 2+, Ba 2+, Cd 2+, Hg 2+, S 2– |
5 |
| Li +, Ca 2+, Cu 2+, Zn 2+, Sn 2+, Mn 2+, Fe 2+, Ni 2+ |
6 |
| Mg 2+, Be 2+ |
8 |
| H +, Al 3+, trivalent rare earths |
9 |
| Th 4+, Zr 4+, Ce 4+ |
11 |
From Garrels and Christ (1982).
This equation is known as the Debye–Hückel limiting law (so-called because it applies in the limit of very dilute concentrations).
Davies (1938, 1962) introduced an empirical modification of the Debye–Hückel equation. The Davies equation is:
(3.77) 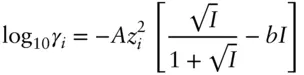
where A is the same as in the Debye–Hückel equation and b is an empirically determined parameter with a value of around 0.3. It is instructive to see how the activity coefficient of Ca 2+would vary according to Debye–Hückel and Davies equations if we vary the ionic strength of the solution. This variation is shown in Figure 3.15. The Davies equation predicts that activity coefficients begin to increase above ionic strengths of about 0.5 m. For reasons discussed below and in greater detail in Chapter 4, activity coefficients do actually increase at higher ionic strengths. On the whole, the Davies equation is slightly more accurate for many solutions at ionic strengths of 0.1−1 m. Because of this, as well as its simplicity, the Davies equation is widely used.
3.7.3.2 Limitations to the Debye–Hückel approach
None of the assumptions made by Debye and Hückel hold in the absolute. Furthermore, the Poisson–Boltzmann equation provides only an approximate description of ion interactions, and Debye and Hückel used an approximate solution of this equation. Thus, we should not expect the Debye–Hückel equations to provide an exact prediction of activity coefficients under all conditions.
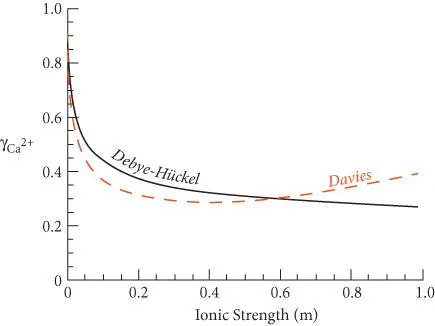
Figure 3.15 Variation of the Ca 2+activity coefficient with ionic strength according to the Debye–Hückel (black solid line) and Davies equations (red dashed line).
Perhaps the greatest difficulty is the assumption of complete dissociation. When ions approach each other closely, the electrostatic interaction energy exceeds the thermal energy, which violates the assumption made in the approximate solution of the Poisson–Boltzmann equation. In this case, the ions are said to be associated. Furthermore, the charge on ions is not spherically symmetric and this asymmetry becomes increasingly important at short distances. Close approach is obviously more likely at high ionic strength, so not surprisingly the Debye–Hückel equation breaks down at high ionic strength.
We can distinguish two broad types of ion associations: ion pairs and complexes. These two classes actually form a continuum, but we will define a complex as an association of ions in solution that involves some degree of covalent bonding (i.e., electron sharing). Ion pairs, on the other hand, are held together purely by electrostatic forces. We will discuss formation of ion pairs and complexes in greater detail in subsequent chapters. Here, we will attempt to convey only a very qualitative understanding of these effects.
An ion pair †can be considered to have formed when ions approach closer than some critical distance where the electrostatic energy, which tends to bind them, exceeds twice the thermal energy, which tends to move them apart. When this happens, the ions are electrostatically bound and their motions are linked. This critical distance depends on the charge of the ions involved and is therefore much greater for highly charged ions than for singly charged ones. As we will show in Chapter 4, ion pairs involving singly charged ions will never form, even at high ionic strengths. On the other hand, multiply charged ions will tend to form ion pairs even at very low ionic strengths.
Formation of ion pairs will cause further deviations from ideality. We can identify two effects. First, the effective concentration, or activity, of an ionic species that forms ionic associations will be reduced. Consider, for example, a pure solution of CaSO 4. If some fraction, α , of Ca 2+and SO 4 2–ions forms ion pairs, then the effective concentration of Ca 2+ions is:
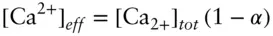
(here we follow the usual convention of using brackets to denote concentrations). The second effect is on ionic strength. By assuming complete dissociation, we similarly overestimate the effective concentration in this example by a factor of (1 – α).
A second phenomenon that causes deviations from ideality not predicted by Debye–Hückel is solvation. As we noted, an ion in aqueous solution is surrounded by a sphere of water molecules that are bound to it. Since those water molecules bound to the ion are effectively unavailable for reaction, the activity of water is reduced by the fraction of water molecules bound in solvation shells. This fraction is trivial in dilution solutions but is important at high ionic strength. The result of this effect is to increase the activity of ions.
Despite these problems, Debye–Hückel has proved to be remarkably successful in predicting activity coefficients in dilute solution. The extended Debye–Hückel equation ( eqn. 3.74) is most useful at concentrations less than 0.1 M, which includes many natural waters, and provides adequate approximation for activity coefficients up to ionic strengths of about 1 M, which would include most solutions of geologic interest, including seawater. As we noted above, the Davies equation is slightly more accurate in the range of 0.1 to 1 M ionic strength. Above these concentrations, both the Davies and Debye–Hückel equations are increasingly inaccurate. There are a variety of geologically important solutions for which the Debye–Hückel and Davies equations cannot be used, including hydrothermal solutions, metamorphic fluids, ore-forming fluids, highly saline lakes, formation brines, and aerosol particles. Figure 3.16summarizes the typical ionic strengths of natural solutions and the applicability of these equations. The Debye–Hückel limiting law is useful only for very dilute solutions, less than 10 −5mol/kg, which is more dilute than essentially all solutions of geologic interest. We will consider several methods of estimating activities in higher ionic strength solutions in Chapter 4.
Читать дальше

 , Ag +
, Ag +
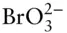 ,
, 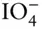 ,
, 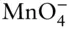
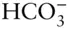 ,
, 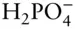 ,
, 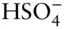 ,
, 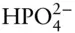 ,
, 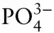
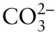 ,
,