William M. White - Geochemistry

Figure 3.16 Ionic strength of natural electrolyte solutions and the applicability of the Debye–Hückel and Davies equations.

Given the composition for the average river water in column A in the table below, calculate the activity of the Ca 2+ion at 25° C using the Debye–Hückel equation.

Answer: Our first step is to convert these concentrations to molality by dividing by the respective molecular weights. We obtain the molal concentrations in column B. We also need to compute z 2(column C), and the product z 2 m (column D). Using equation 3.75, we calculate the ionic strength to be 0.00202 m. (Note, one must use the ionic strength in molal or molar, and not millimolar, units in the Debye–Hückel Equation.

	A	B	C	D
Ion	g/kg	mol/kg × 10 3	z 2	mz 2× 10 3
Cl –	0.0078	0.2201	1	0.2201
	0.0112	0.1167	4	0.4667
HCO	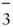0.0583	0.9557	1	0.9557
Mg 2+	0.0041	0.1687	4	0.6746
Ca 2+	0.015	0.3742	4	1.4970
K +	0.0023	0.0588	1	0.0588
Na +	0.0041	0.1782	1	0.1782

We substitute this value for I, then find å = 6, A = 0.5092, and B = 0.3283 in Table 3.1, and obtain a value for the activity coefficient of 0.8237, and an activity of 0.308 ×10 −3m. If we did the calculation for other temperatures, we would see that for a dilute solution such as this, the activity coefficient is only a weak function of temperature, decreasing to 0.625 at 300° C.

When we deal with solid solutions, we are again faced with the inadequacy of the purely macroscopic approach of classical thermodynamics. There is little disadvantage to this approach for gases, where the arrangement of molecules is chaotic. But the crystalline state differs from that of gases in that the arrangement of atoms in the crystal lattice is highly ordered, and the properties of the crystal depend strongly on the nature of the ordering. For this reason, we cannot afford to ignore the arrangement of atoms in solids, particularly with respect to solutions.

Solid solutions differ from those of gases and liquids in several respects. First, solution in the solid state inevitably involves substitution. While we can increase the concentration of HCl in water simply by adding HCl gas, we can only increase the concentration of Fe in biotite solid solution if we simultaneously remove Mg. Second, solid solutions involve substitution at crystallographically distinct sites. Thus, in biotite a solid solution between phlogopite (KMg 3AlSi 3O 10(OH) 2) and annite (KFe 3AlSi 3O 10(OH) 2) occurs as Fe 2+replaces Mg 2+in the octahedral site; the tetrahedral Si site and the anion (O) sites remain unaffected by this substitution. Third, substitution is often coupled. For example, the solid solution between anorthite (CaAl 2Si 2O 8) and albite (NaAlSi 3O 8) in plagioclase feldspar involves not only the substitution of Na +for Ca 2+, but also the substitution of Al 3+for Si 4+. The anorthite–albite solution problem is clearly simplified if we choose anorthite and albite as our components rather than Na +, Ca 2+, Al 3+and Si 4+. Such components are known as phase components . Choosing pure phase end members as components is not always satisfactory either because substitution on more than one site is possible, leading to an unreasonably large number of components, or because the pure phase does not exist and hence its thermodynamic properties cannot be measured.

However we choose our components, we need a method of calculating activities that takes account of the ordered nature of the crystalline state. Here we will discuss two ideal solution models of crystalline solids. We tackle the problem of nonideal solid solutions in Chapter 4.

Many crystalline solids can be successfully treated as ideal solutions. Where this is possible, the thermodynamic treatment and assessment of equilibrium are greatly simplified. A simple and often successful model that assumes ideality but takes account of the ordered nature of the crystalline state is the mixing-on-site model , which considers the substitution of species in sites individually. In this model, the activity of an individual species is calculated as:

(3.78)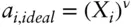

where X is the mole fraction of the i thatom and ν is the number of sites per formula unit on which mixing takes place. For example, ν = 2 in the Fe–Mg exchange in olivine, (Mg,Fe) 2SiO 4. One trick to simplifying this equation is to pick the formula unit such that ν = 1. For example, we would pick (Mg,Fe)Si ½O 2as the formula unit for olivine. We must then consistently choose all other thermodynamic parameters to be half those of (Mg,Fe) 2SiO 4.

The entropy of mixing is given by:

(3.79)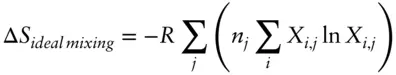

where the subscript j refers to sites and the subscript i refers to components, and n is the number of sites per formula unit. The entropy of mixing is the same as the configurational entropy, residual entropy, or “third law entropy” (i.e., entropy when T = 0 K). For example, in clinopyroxene, there are two exchangeable sites, a sixfold-coordinated M1 site, (Mg, Fe 2+, Fe 3+, Al 3+), and an eightfold-coordinated M2 site (Ca 2+, Na +). Here j ranges from 1 to 2 (e.g., 1 = M1, 2 = M2), but n = 1 in both cases (because both sites accept only one atom). i must range over all present ions in each site, so in this example, i ranges from 1 to 4 (1 = Mg, 2 = Fe 2+, etc.) when j = 1 and from 1 to 2 when j = 2. Since we have assumed an ideal solution, ΔH = 0 and ΔG ideal = −TΔS . In other words, all we need is temperature and eqn. 3.79to calculate the free energy of solution.

In the mixing-on-site model, the activity of a phase component in a solution, for example, pyrope in garnet, is the product of the activity of the individual species in each site in the phase:

(3.80)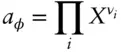

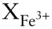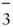
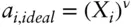
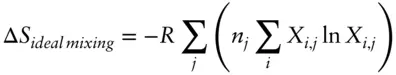
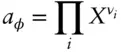
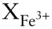where a φis the activity of phase component φ , i are the ion components of pure φ , and ν iis the stoichiometric proportion of i in pure φ . For example, to calculate the activity of aegirine (NaFe 3+Si 2O 6) in aegirine-augite ([Na,Ca][Fe 3+,Fe 2+,Mg]Si 2O 6), we would calculate the product: X Na . Note that it would not be necessary to include the mole fractions of Si and O, since these are 1 (see Example 3.4).