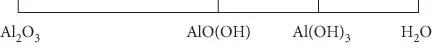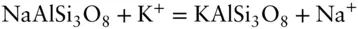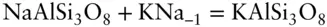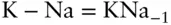In contrast to a species, a component need not be a real chemical entity; rather, it is simply an algebraic term in a chemical reaction. The minimum number of components †of a system is rigidly defined as the minimum number of independently variable entities necessary to describe the composition of each and every phase of a system . Unlike species and phases, components may be defined in any convenient manner: what the components of your system are and how many there are depend on your interest and on the level of complexity you will be dealing with. Consider our aragonite–calcite fossil. If the only reaction occurring in our system (the fossil) is the transformation of aragonite to calcite, one component, CaCO 3, is adequate to describe the composition of both phases. If, however, we are also interested in the precipitation of calcium carbonate from water, we might have to consider CaCO 3as consisting of two components: Ca 2+and 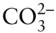 .
.
There is a rule to determine the minimum number of components in a system once you decide what your interest in the system is; the hard part is often determining your interest. The rule is:
(3.1) 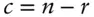
where n is the number of species and r is the number of independent chemical reactions possible between these species . Essentially, this equation simply states that if a chemical species can be expressed as the algebraic sum of other components, we need not include that species among our minimum set of components. Let's try the rule on the species we listed above for water. We have six species: H 2O, H 2CO 3, 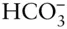 ,
, 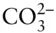 , H +, and OH –.
, H +, and OH –.
We can write three reactions relating them:
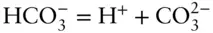
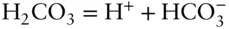

Equation 3.1tells us we need 3 = 6 – 3 components to describe this system: 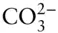 , H +, and OH –. Put another way, we see that carbonic acid, bicarbonate, and water can all be expressed as algebraic sums of hydrogen, hydroxyl, and carbonate ions, so they need not be among our minimum set of components.
, H +, and OH –. Put another way, we see that carbonic acid, bicarbonate, and water can all be expressed as algebraic sums of hydrogen, hydroxyl, and carbonate ions, so they need not be among our minimum set of components.
In igneous and metamorphic petrology, components are often the major oxides (though we may often choose to consider only a subset of these). On the other hand, if we were concerned with the isotopic equilibration of minerals with a hydrothermal fluid, 18O might be considered as a different component than 16O.
Perhaps the most straightforward way of determining the number of components is a graphical approach. If all phases can be represented on a one-dimensional diagram (that is, a straightline representing composition), we are dealing with a two-component system. For example, consider the hydration of Al 2O 3(corundum) to form boehmite (AlO(OH)) or gibbsite Al(OH) 3. Such a system would contain four phases (corundum, boehmite, gibbsite, water), but is nevertheless a two-component system because all phases may be represented in one dimension of composition space, as shown in Figure 3.1. Because there are two polymorphs of gibbsite, one of boehmite, and two other possible phases of water, there are nine possible phases in this two-component system. Clearly, a system may have many more phases than components.
Similarly, if a system may be represented in two dimensions, it is a three-component system. Figure 3.2is a ternary diagram illustrating the system Al 2O 3–H 2O–SiO 2. The graphical representation approach reaches its practical limit in a four-component system because of the difficulty of representing more than three dimensions on paper. A four-component system is a quaternary one, and can be represented with a three-dimensional quaternary diagram.
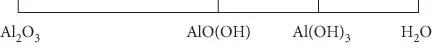
Figure 3.1 Graphical representation of the system Al 2O 3−H 2O.
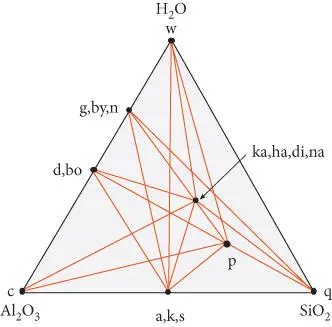
Figure 3.2 Phase diagram for the system Al 2O 3–H 2O–SiO 2. The lines are called joins because they join phases. In addition to the end-members, or components, phases represented are g : gibbsite, by : bayerite, n : norstrandite (all polymorphs of Al(OH) 3), d: diaspore, bo : boehmite (polymorphs of AlO(OH)), a : andalusite, k : kyanite, s : sillimanite (all polymorphs of Al 2SiO 5), ka : kaolinite, ha : halloysite, di : dickite, na : nacrite (all polymorphs of Al 2Si 2O 5(OH) 4), and p : pyrophyllite (Al 2Si 4O 10(OH) 2). There are also six polymorphs of quartz, q (coesite, stishovite, tridymite, cristobalite, α-quartz, and β-quartz).
It is important to understand that a component may or may not have chemical reality. For example in the exchange reaction:
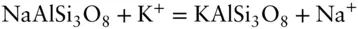
we could alternatively define the exchange operator KNa −1(where Na −1is −1 mol of Na ion) and write the equation as:
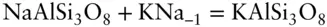
In addition, we can also write the reaction:
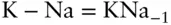
Here we have four species and two reactions and thus a minimum of only two components. You can see that a component is merely an algebraic term .
There is generally some freedom in choosing components. For example, in the ternary (i.e., three-component) system SiO 2−Mg 2SiO 4−MgCaSi 2O 6, we could choose our components to be quartz, diopside, and forsterite, or we could choose them to be SiO 2, MgO, and CaO. Either way, we are dealing with a ternary system (which contains MgSiO 3as well as the three other phases).
3.2.1.4 Degrees of freedom
The number of degrees of freedom in a system is equal to the sum of the number of independent intensive variables (generally temperature and pressure) and independent concentrations (or activities or chemical potentials) of components in phases that must be fixed to define uniquely the state of the system. A system that has no degrees of freedom (i.e., is uniquely fixed) is said to be invariant, one that has one degree of freedom is univariant, and so on. Thus, in a univariant system, for example, we need specify the value of only one variable, for example, temperature or the concentration of one component in one phase, and the value of pressure and all other concentrations are then fixed and can be calculated (assuming the system is at equilibrium).
Читать дальше

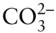 .
.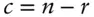
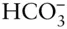 ,
, 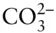 , H +, and OH –.
, H +, and OH –.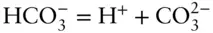
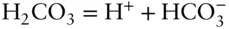

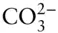 , H +, and OH –. Put another way, we see that carbonic acid, bicarbonate, and water can all be expressed as algebraic sums of hydrogen, hydroxyl, and carbonate ions, so they need not be among our minimum set of components.
, H +, and OH –. Put another way, we see that carbonic acid, bicarbonate, and water can all be expressed as algebraic sums of hydrogen, hydroxyl, and carbonate ions, so they need not be among our minimum set of components.