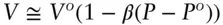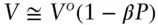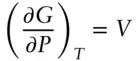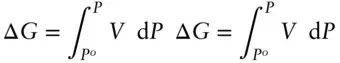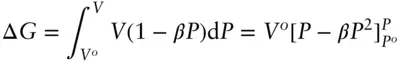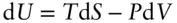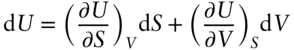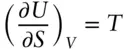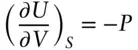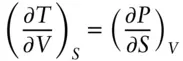However, the value of P−P ois of the order of 10 –2, and in this case, the approximation 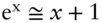 holds, so that eqn. 2.139may be written as:
holds, so that eqn. 2.139may be written as:
(2.140) 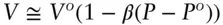
equation 2.140is a general expression that expresses volume as a function of pressure when β is known, small, and is independent of temperature and pressure. Furthermore, in situations where P > P o, this can be simplified to:
(2.141) 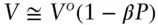
Using equation 2.141, we calculate a molar volume of 43.54 cc/mol (identical to the value obtained using eqn. 2.139). The volume change, Δ V , is 0.04 cc/mol.
The change in free energy with volume is given by:
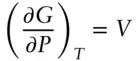
so that the free energy change as a consequence of a finite change is pressure can be obtained by integrating:
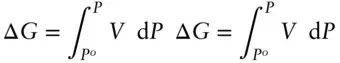
Into this we may substitute eqn. 2.141:
(2.142) 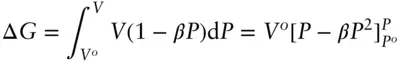
Using eqn. 2.142we calculate a value of ΔG of 4.37 kJ/mol.
2.12 THE MAXWELL RELATIONS*
The reciprocity *relationship, which we discussed earlier, leads to a number of useful relationships. These relationships are known as the Maxwell relations. Consider the equation:
(2.58) 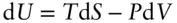
If we write the partial differential of U in terms of S and V we have:
(2.143) 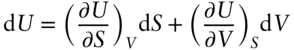
From a comparison of these two equations, we see that:
(2.144a) 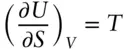
and
(2.144b) 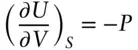
And since the cross-differentials are equal, it follows that:
(2.145) 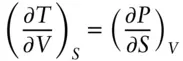
The other Maxwell relations can be derived in an exactly analogous way from other state functions. They are:
From dH (eqn 2.65):(2.146)
from dA ( eqn. 2.121)(2.147)
from dG ( eqn. 2.122)(2.148)
In this chapter, we introduced the fundamental variables and laws of thermodynamics.
Temperature, pressure, volume, and energy are state variables who value depends only on the state of the system and not the path taken to that state. Two other fundamental variables, work and heat, are not state variables and their value is path dependent in transformations. Relationships between state variables are known as equations of state. Most often we are interested in changes in state variables rather than their absolute values and we often express these in terms of partial differential equations, for example, the dependence of volume on T and P is written as:(2.17)
The first law states the principle of conservation of energy: even though work and heat are path dependent, their sum is the energy change in a transformation and is path independent:(2.22)
We introduced another important state variable, entropy, which is a measure of the randomness of a system and is defined as:(2.47) where Ω is the number of states accessible to the system and k is Boltzmann's constant.
The second law states that in any real transformation the increase in entropy will always exceed the ratio of heat exchanged to temperature:(2.51) In the fictional case of a reversible reaction, entropy change equals the ratio of heat exchanged to temperature.
The third law states that the entropy of a perfectly crystalline substance at the absolute 0 of temperature is 0. Any other substance will have a finite entropy at absolute 0, which is known as the configurational entropy:(2.110)
We then introduced another useful variable, H, the enthalpy, which can be thought of as the heat content of a system and is related to other state variables as:(2.65) The value of enthalpy is in measuring the energy consumed or released in changes of state of a system, including phase changes such as melting.
The heat capacity of a system, C, is the amount of heat required to raise its temperature. This will depend on whether volume or pressure is held constant. For the latter:(2.68)
With these variables, we could then define a particularly useful state function called the Gibbs free energy, G:(2.125) Written in terms of its characteristic variables:(2.124) The Gibbs free energy is the amount of energy available to drive chemical transformations. It has two important properties:Produces and reactants are in equilibrium when the Gibbs free energies are equal and At fixed temperature and pressure, a chemical reaction will proceed in the direction of lower Gibbs free energy.
REFERENCES AND SUGGESTIONS FOR FURTHER READING
1 Anderson, G.M. and Crerar, D.A. 1993. Thermodynamics in Geochemistry. New York, Oxford University Press.
2 Berman, R.G. 1988. Internally-consistent thermodynamic data for minerals in the system Na2O-K2O-CaO-MgO-FeO-Fe2O3-Al2O3-SiO2-TiO2-H2O-CO2. Journal of Petrology 29, 445–552.
3 Einstein, A. 1905. Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig? Annalen der Physik 18, 639–643.
4 Feynman, R., Leighton, R.B. and Sands, M.L. 1989. The Feynman Lectures on Physics Vol. I. Pasadena: California Institute of Technology.
5 Fletcher, P. 1993. Chemical Thermodynamics for Earth Scientists. Essex: Longman Scientific and Technical.
6 Haas, J.L. and Fisher, J.R. 1976. Simultaneous evaluation and correlation of thermodynamic data. American Journal of Science 276: 525–45.
7 Helgeson, H.C., Delany, J.M., Nesbitt, H.W. and Bird, D.K. 1978. Summary and critique of the thermodynamic properties of rock-forming minerals. American Journal of Science 278A: 1–229.
8 Holland, T. J. B. and Powell, R. 1998. An internally consistent thermodynamic data set for phases of petrological interest. Journal of Metamorphic Geology 16(3), 309–343. doi: 10.1111/j.1525-1314.1998.00140.x.
9 Nordstrom, D.K. and Munoz, J.L. 1986. Geochemical Thermodynamics. Palo Alto, Blackwell Scientific.
1 For a pure olivine mantle, calculate the adiabatic temperature gradient (∂T/∂P)s at 0.1 MPa (1 atm) and 1000°C. Use the thermodynamic data in Table 2.2for forsterite (Mg-olivine, Mg2SiO4), and , and .Note that: 1 cc/mol = 1 J/MPa/mol.
Читать дальше

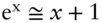 holds, so that eqn. 2.139may be written as:
holds, so that eqn. 2.139may be written as: