(3.7) 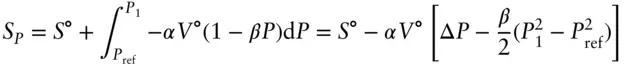
The reference pressure, P ref, is negligible compared with P 1(0.1 MPa vs 1600 MPa), so that this simplifies to:
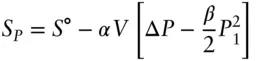
For graphite, S pis 5.66 J/K-mol, for diamond it is 2.34 J/K-mol, so Δ S rat 1600 MPa is −3.32 J-K −1-mol −1.
The Clapeyron slope is therefore:
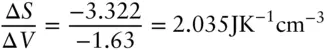
One distinct advantage of the SI units is that cm 3= J/MPa, so the above units are equivalent to K/MPa. From this, the pressure of the phase change at 1000°C can be calculated as:
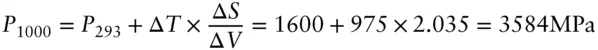
The Clapeyron slope we calculated (solid line) is compared with the experimentally determined phase boundary in Figure 3.3. Our calculated phase boundary is linear whereas the experimental one is not. The curved nature of the observed phase boundary indicates Δ V and Δ S are pressure- and temperature-dependent. This is indeed the case, particularly for graphite. A more accurate estimate of the volume change requires that β be expressed as a function of pressure.

Figure 3.3 Comparison of the graphite–diamond phase boundary calculated from thermodynamic data and the Clapeyron slope (solid line) with the experimentally observed phase boundary (dashed line).
Solutions are defined as homogeneous phases produced by dissolving one or more substances in another substance . In geochemistry we are often confronted by solutions: as gases, liquids, and solids. Free energy depends not only on T and P , but also on composition. In thermodynamics it is generally most convenient to express compositions in terms of mole fractions, X i , the number of moles of i divided by the total moles in the substance (moles are weight divided by atomic or molecular weight). The sum of all the X ifractions must, of course, total to 1.
Solutions are distinct from purely mechanical mixtures. For example, salad dressing (oil and vinegar) is not a solution. Similarly, we can grind anorthite (CaAl 2Si 2O 8) and albite (NaAlSi 3O 8) crystals into a fine powder and mix them, but the result is not a plagioclase solid solution. The Gibbs free energy of mechanical mixtures is simply the sum of the free energy of the components. If, however, we heated the anorthite–albite mixture to a sufficiently high temperature that the kinetic barriers were overcome, there would be a reordering of atoms and the creation of a true solution. Because this reordering is a spontaneous chemical reaction, there must be a decrease in the Gibbs free energy associated with it. This solution would be stable at 1 atm and 25°C. Thus, we can conclude that the solution has a lower Gibbs free energy than the mechanical mixture. On the other hand, vinegar will never dissolve in oil at 1 atm and 25°C because the Gibbs free energy of that solution is greater than that of the mechanical mixture.
Working with solutions of ethylene bromide and propylene bromide, Raoult §noticed that the vapor pressures of the components in a solution were proportional to the mole fractions of those components:
(3.8) 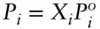
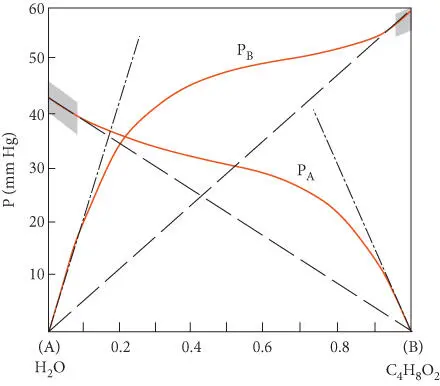
Figure 3.4 Vapor pressure of water and dioxane in a water–dioxane mixture showing deviations from ideal mixing. Shaded areas are areas where Raoult's law (dashed lines). Henry's law slopes are shown as dot-dashed lines. After Nordstrom and Munoz (1986).
where P iis the vapor pressure of component i above the solution, X iis the mole fraction of i in solution, and 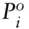 is the vapor pressure of pure i under standard conditions. Assuming the partial pressures are additive and the sum of all the partial pressures is equal to the total gas pressure (Σ P i= P total):
is the vapor pressure of pure i under standard conditions. Assuming the partial pressures are additive and the sum of all the partial pressures is equal to the total gas pressure (Σ P i= P total):
(3.9) 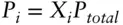
Thus, partial pressures are proportional to their mole fractions. This is the definition of the partial pressureof the i thgas in a mixture.
Raoult's law holds only for ideal solutions, that is, substances where there are no intermolecular forces. It also holds to a good approximation where the forces between like molecules are the same as between different molecules. The two components Raoult was working with were very similar chemically, so that this condition held, and the solution was nearly ideal. As you might guess, not all solutions are ideal. Figure 3.4shows the variations of partial pressures above a mixture of water and dioxane. Significant deviations from Raoult's law are the rule except where X iapproaches 1.
Another useful approximation occurs when X iapproaches 0. In this case, the partial pressures are not equal to the mole fraction times the vapor pressure of the pure substance, but they do vary linearly with X i. This behavior follows Henry's law, *which is:
(3.10) 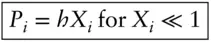
where h is known as the Henry's law constant.
3.4 CHEMICAL POTENTIAL
3.4.1 Partial molar quantities
Free energy and other thermodynamic properties are dependent on composition. We need a way of expressing this dependence. For any extensive property of the system, such as volume, entropy, energy, or free energy, we can define a partial molar value , which expresses how that property will depend on changes in amount of one component. For example, we define the partial molar volume of component i in phase φ as:
(3.11) 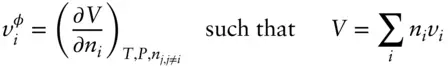
(we will use small letters to denote partial molar quantities; the superscript refers to the phase and the subscript refers to the component). The plain language interpretation of eqn. 3.11is that the partial molar volume of component i in phase φ tells us how the volume of phase φ will vary with an infinitesimal addition of component i , if all other variables are held constant . For example, the partial molar volume of Na in an aqueous solution such as seawater would tell us how the volume of that solution would change for an infinitesimal addition of Na. In this case i would refer to the Na component and φ would refer to the aqueous solution phase. In Table 2.2, we see that the molar volumes of the albite and anorthite end-members of the plagioclase solid solution are different. We could define 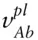 as the partial molar volume of albite in plagioclase, which would tell us how the volume of plagioclase would vary for an infinitesimal addition of albite. (In this example, we have chosen our component as albite rather than Na. While we could have chosen Na, the choice of albite simplifies matters because the replacement of Na with Ca is accompanied by the replacement of Si by Al.)
as the partial molar volume of albite in plagioclase, which would tell us how the volume of plagioclase would vary for an infinitesimal addition of albite. (In this example, we have chosen our component as albite rather than Na. While we could have chosen Na, the choice of albite simplifies matters because the replacement of Na with Ca is accompanied by the replacement of Si by Al.)
Читать дальше

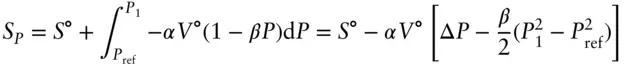
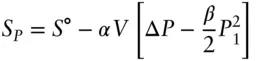
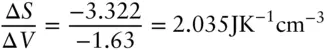
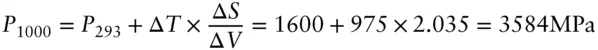

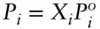

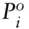 is the vapor pressure of pure i under standard conditions. Assuming the partial pressures are additive and the sum of all the partial pressures is equal to the total gas pressure (Σ P i= P total):
is the vapor pressure of pure i under standard conditions. Assuming the partial pressures are additive and the sum of all the partial pressures is equal to the total gas pressure (Σ P i= P total):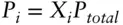
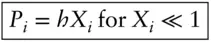
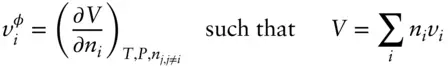
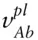 as the partial molar volume of albite in plagioclase, which would tell us how the volume of plagioclase would vary for an infinitesimal addition of albite. (In this example, we have chosen our component as albite rather than Na. While we could have chosen Na, the choice of albite simplifies matters because the replacement of Na with Ca is accompanied by the replacement of Si by Al.)
as the partial molar volume of albite in plagioclase, which would tell us how the volume of plagioclase would vary for an infinitesimal addition of albite. (In this example, we have chosen our component as albite rather than Na. While we could have chosen Na, the choice of albite simplifies matters because the replacement of Na with Ca is accompanied by the replacement of Si by Al.)










