Mickael Launay - It All Adds Up

From that point on, numbers became an abstract concept, and that is what gave mathematics its identity: it is the science of abstraction par excellence. The objects that mathematics studies do not have a physical existence. They are not material, they are not made of atoms, they’re purely ideas. And yet these ideas are remarkably effective when it comes to making sense of the world.

It is undoubtedly no accident that the need to be able to write down numbers acted at the time as a determining factor in the emergence of writing. While other ideas could be transmitted orally without any problem, it seemed on the other hand difficult to establish a system of numbers without moving to a written notation.

Can we, even today, dissociate the idea we have of numbers from our written representation of them? If I ask you to think of a sheep, how do you see it? You probably represent it as a bleating animal with four legs and a woolly back. You would never think of visualizing the five letters of the word ‘sheep’. Yet if I talk now about the number one hundred and twenty-eight, what do you see? Do the 1, the 2 and the 8 take shape in your brain and come together as though they are written in the intangible ink of your thoughts? Our mental representation of large numbers appears to be definitively linked to their written form.

This example came out of the blue. Although for everything else, writing was just a means of transcribing something that had previously existed in the spoken language, now, in the case of numbers, it was the writing that would dictate the language. Think about it: when you pronounce ‘One hundred and twenty-eight’, you are just reading 128: 100 + 20 + 8. Above a certain threshold, it becomes impossible to speak about numbers without the written medium. Before they were written down, there were no words for large numbers.

To this day, some indigenous peoples still only have a very limited number of words for designating numbers. For example, the members of the Pirahã tribe of hunter-gatherers who live on the banks of the Maici River in Amazonia only count to two. Above that, they use a single word signifying ‘several’ or ‘many’. Again in Amazonia, the Munduruku only have words for up to five – that is to say a hand.

In our modern societies, numbers have invaded our everyday lives. They have become so omnipresent and indispensable that we often forget just how brilliant the idea is, and that it took our ancestors centuries to provide us with evidence of this.

Throughout the ages, very many procedures for recording numbers have been invented. The simplest of these involves writing down as many signs as the desired number – for example, a sequence of bars side by side. We often still use this method, for example to count the points in a game.

The oldest known indication of the probable use of this procedure dates back to well before the invention of writing by the Sumerians. The so-called Ishango bone (actually two baboon bones) was found in the 1950s on the shores of Lake Edward in what is now the Democratic Republic of Congo and dates back some twenty thousand years. The bones are 10 and 14 centimetres long, and feature a large number of more or less regularly spaced incisions. What was the role of these incisions? It is likely that this was a first counting system. Some people think the bones are a calendar, while others extrapolate an already highly advanced knowledge of arithmetic. It is hard to know for sure. The two bones are now on display in the museum of the Royal Belgian Institute of National Sciences in Brussels.

This method of counting using a mark for each unit added rapidly reached its limits as soon as there was a need to manipulate relatively large numbers. Packets were introduced to achieve a greater speed.

The Mesopotamian tokens could already represent several units. For example, there was a particular token for representing ten sheep. This principle was retained at the time that writing came in. There are symbols to denote packets of 10, of 60, of 600, of 3,600 and of 36,000.

Here we also see the search for a logic in the construction of the symbols. For example, the 60 and the 3,600 are multiplied by 10 when a circle is included inside them. With the arrival of cuneiform writing, these first symbols were gradually transformed into the following:

Because it was so close to Mesopotamia, Egypt did not lag far behind in adopting writing, and developed its own numeration symbols from the start of the third millennium.

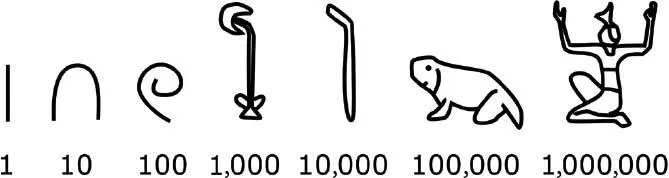
The system was then purely decimal: each symbol had a value ten times greater than the one before.

These additive systems, in which one just has to add the values of the written symbols, became very popular throughout the world, and numerous variants were unveiled throughout antiquity and also much of the Middle Ages. They were used, in particular, by the Greeks and the Romans, who simply employed the letters of their respective alphabets as numerical symbols.

Alongside the additive systems, a new form of notation for numbers gradually emerged: numeration by position. In these systems, the value of a symbol was defined to depend on the position it occupies within the number. Once again, the Mesopotamians were the first to come up with this.

In the second millennium BC, it was the town of Babylon that now shone brightly over the Near East. Cuneiform writing was still in vogue, but now, just two symbols were used: the simple nail that had the value ‘1’ and the chevron with the value ‘10’.

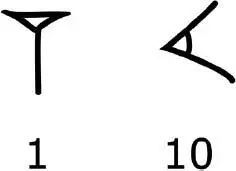
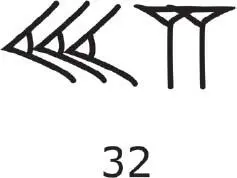
These two signs were used to provide an additive notation for all numbers up to 59. For example, the number 32 was written as three chevrons followed by two nails.

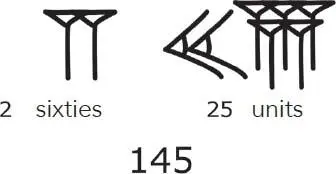
Then, from 60 onwards, groups were introduced, where the same symbols were used to denote groups of 60. Thus, in the same way as in our present-day notation, where the figures read from right to left denote the units, then the tens, then the hundreds, in this Babylonian numeration the units are read first, then the sixties, then the three-thousand-six-hundreds (that is, sixty sixties), and so on, where each rank has a value sixty times greater than its predecessor.

For example, the number 145 consists of two sixties (which make 120) to which you have to add 25 units. The Babylonians would therefore have denoted it as follows:

Based on this system, Babylonian scholars developed an extraordinary knowledge. They had a good understanding of the four basic operations of addition, subtraction, multiplication and division, and also of square roots, powers and reciprocals. They produced extremely detailed arithmetic tables and developed very good solution techniques for equations that they set themselves.