Mickael Launay - It All Adds Up

However, all this was soon forgotten. The Babylonian civilization was in decline, and a large part of its mathematical advances would be consigned to oblivion. There would be no more numeration by position and no more equations. Indeed, there was a time lag of centuries before these questions became the flavour of the day again, and it was only in the nineteenth century that the decoding of cuneiform tablets reminded us that the Mesopotamians had tackled these things before everyone else.

Following the Babylonians, the Mayans also devised a positional system, in this case with base 20. Then it was the turn of the Indians to invent a system with base 10. This last system was used by Arab scholars before it reached Europe at the end of the Middle Ages. Its symbols became known as Arabic figures, and soon spread all over the world.

0 1 2 3 4 5 6 7 8 9

With numbers, mankind gradually came to understand that it had just invented a tool for describing, analysing and understanding the world around it that surpassed any purpose it might have hoped for.

Sometimes we have been so pleased with numbers that we have even overdone it. The birth of numbers represented at the same time the birth of the practice of various forms of numerology. This involves attributing magical properties to numbers, interpreting them beyond the bounds of reason, and attempting to read into them messages from the gods and about the fate of the world.

In the sixth century BC, the Greek scholar Pythagoras made numbers the fundamental concept of his philosophy when he declared: ‘Everything is a number.’ According to him, it is numbers that produce geometric figures, which in turn give rise to the four elements of matter – fire, water, earth and air – of which all living things are made. Pythagoras thus created a whole system around numbers. The odd numbers were associated with the masculine, while the even numbers were feminine. The number 10, represented as a triangle called the tetractys , became a symbol of harmony and of the perfection of the cosmos. Pythagoreans were also behind the origin of arithmancy, which claimed to read people’s characters by associating numerical values with the letters comprising their names.

In parallel, there began to be discussions about what constitutes a number. Some authors believed that the unit – 1 – is not a number, because a number denotes a plurality and so can only be considered from 2 onwards. It was even asserted that in order for it to be able to generate all the other numbers, 1 must be simultaneously even and odd.

Later, increasingly animated discussions developed concerning the zero, the negative numbers and the imaginary numbers. In each case, the admission of these new ideas to the circle of numbers led to debate and forced mathematicians to broaden their ideas.

In short, numbers have never ceased to raise questions, and human beings still need time to learn to master these strange creatures that are their brainchildren.

Once numbers had been invented, it did not take long for the discipline of mathematics to spread its wings. Various core branches such as arithmetic, logic and algebra gradually sprouted within it, developed to maturity and asserted themselves as disciplines in their own right.

One of these, geometry, rapidly won the popularity stakes and captivated the greatest scholars of antiquity. It was this that singled out the first celebrities of mathematics, such as Thales, Pythagoras and Archimedes, whose names still haunt the pages of our textbooks.

However, before it became a subject for great minds, geometry gained its place on the ground. Its etymology bears witness to this: it is first and foremost the science of the measurement of the Earth, and the first surveyors were hands-on mathematicians. Problems concerning the division of territory were then classics of the craft. How to divide a field into equal parts? How to determine the price of a plot of land from its area? Which of two plots is closer to the river? What route should the future canal follow to make it the shortest possible?

All these questions were paramount in ancient societies where the whole economy still revolved in a vital way around agriculture and hence around the distribution of land. In response to this, geometrical know-how was built up, enriched and transmitted from generation to generation. Anyone equipped with this know-how was certain to hold a central and indisputable place in society.

For these measurement professionals, the rope was often the primary instrument of geometry. In Egypt, ‘ropestretcher’ was a profession in its own right. When the Nile floods led to regular inundations, it was the ropestretchers who were sent for to redefine the boundaries of plots that bordered the river. Using information they recorded about the ground, they planted their stakes, stretched their long ropes across the fields, and then carried out calculations that enabled them to rediscover the boundaries erased by the floodwaters.

They were also the first port of call in constructing buildings, when they took the measurements on the ground and marked the precise location of the building based on architects’ plans. And in the case of a temple or an important monument, it was often the pharaoh in person who symbolically came to stretch the first rope.

It can be said that the rope was the all-purpose tool of geometry. Surveyors used it as a ruler, as compasses, and as a set-square.

To use it as a ruler is straightforward: if you stretch the rope between two fixed points you obtain a straight line. And if you require a graduated ruler, you just tie knots at regular intervals along your rope. For compasses, there is no magic involved either. You simply fix one of the two ends to a stake, stretch the rope and move the other end around the stake. This gives a circle. And if your rope is graduated, you can control the length of the radius exactly.

For the set-square, however, things are slightly more complicated. Let’s look at this particular problem for a few moments: what would you do to draw a right angle? With a bit of research, one can come up with several different methods. If, for example, you draw two circles that intersect each other, then the straight line that joins their centres is perpendicular to the straight line that passes through their two points of intersection. There is your right angle.

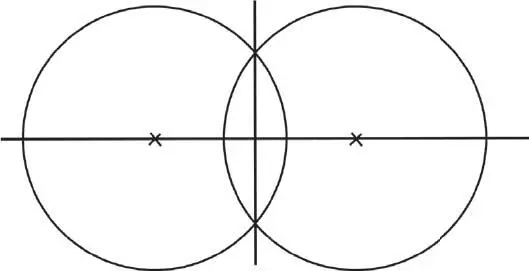
From a theoretical point of view, this construction works perfectly, but things are more complicated in practice. Imagine the surveyors, out in the fields, having to lay out two large circles precisely every time they needed to draw a right angle or, more simply, to verify that an angle which had already been constructed was actually a right angle. This was neither fast nor efficient.