Mickael Launay - It All Adds Up

Finally, the seventh category consists of friezes that have a vertical symmetry, a centre of rotation and a glide symmetry.

Note that these categories only relate to the geometric structure of the friezes and do not exclude possible variations in the pattern designs. Thus, while the following friezes are all different, they all belong to the seventh category.

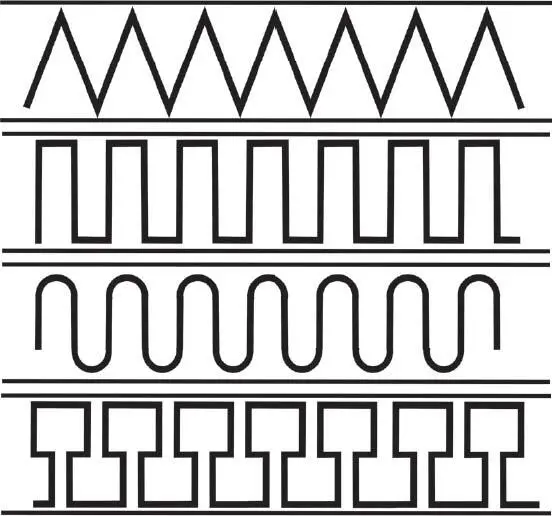
Therefore, all the friezes that you can possibly imagine belong to one of these seven categories. Any other combination is geometrically impossible. Curiously, the last two categories are the most common. It is spontaneously easier to draw figures with a lot of symmetries than figures that have only a few.

Bursting with pride following my successes with the Mesopotamians, I am back the very next day, ready to take ancient Greece by storm. I have barely arrived and already I am overwhelmed with choice. The hunt for friezes here is child’s play. After just a few steps, a few display cases and a few black amphoras decorated with red figures, I have already found my list of seven friezes again.

Faced with such an abundance of riches, I quickly decide not to record my statistics as I had done in Mesopotamia. I am amazed by the creativity of the artists. Ever more complex and ingenious new patterns come into view. I have to pause several times and concentrate hard in order to unravel in my mind all the intertwined visions that are swirling around me.

In one room, a loutrophoros with red figures takes my breath away. A loutrophoros is a tall slender vase with two handles; its function is to carry water for bathing – this one is almost one metre tall. The friezes come thick and fast, and I begin by ticking them off by category. One. Two. Three. Four. Five. In a few seconds I have identified five of the seven geometric structures. The vase is standing against the wall, but when I lean over I can see that it has a frieze of the sixth category on its hidden face. I’m missing just one frieze now. That would be too much to ask. Surprisingly, the missing one is not the same one as the day before. Times have changed, and fashions too; I’m no longer missing the glide symmetry, but the combination comprising vertical symmetry, rotation and glide symmetry.

I am looking frantically for it, my eyes scanning each and every feature of the object. But I can’t find it. I’m slightly disappointed and preparing to give up when my gaze alights on a detail. In the middle of the vase there is a depiction of a scene involving two people. At first sight, there does not seem to be a frieze at that point. Then, an object at the bottom right-hand corner of the scene stops me in my tracks: a vase on which the central person is resting. A vase drawn on the vase! This technique of mise en abyme , in which an image contains a smaller copy of itself, makes me smile. I look closer. The image is a little damaged, but there is no doubt about it: this image of a vase itself contains a frieze and, what a miracle, it’s the one that I’m missing!

Despite my repeated efforts I will fail to find another piece with the same property. This loutrophoros seems to be unique in the Louvre’s collections: it is the only one that bears all seven categories of friezes.

A little further on, another surprise awaits me: friezes in 3D! And I had thought perspective was an invention of the Renaissance. Bright and dark areas skilfully positioned by the artist create a chiaroscuro effect, adding volume to the geometric shapes that pursue each other around the circumference of this gigantic receptacle.

The further I proceed, the more questions arise. Some pieces are not covered by friezes but by tilings. In other words, the geometric patterns no longer simply fill a narrow band running around the object, but now also invade its whole surface, thereby reducing the possibilities for geometric combinations.

After the Greeks come the Egyptians, the Etruscans and the Romans. I discover illusions of filigree lace carved in stone. The stone threads are interwoven and pass alternately above and below one another in a perfectly regular meshing. Then, as if the works of art are not sufficient in themselves, I am soon surprised to find myself observing the Louvre itself, its ceilings, its tiled floors and its door surrounds. As I return home, it’s as though I am unable to stop myself. In the street, I look at the balconies of buildings, the patterns on the clothes worn by passers-by, the walls in the corridors of the Métro, etc.

You have only to change how you look at the world to see mathematics emerge. The search is fascinating. It has no end.

And the adventure is just beginning.

In those days, in Mesopotamia, the region was thriving. At the end of the fourth millennium BC, the small villages we visited earlier had transformed into flourishing towns. Some of them now already had several tens of thousands of inhabitants. Technology was advancing at a rate never before seen. Artisans, whether they were architects, goldsmiths, potters, weavers, carpenters or sculptors, needed to exhibit constant ingenuity to cope with the technical challenges they confronted. Metallurgy was not yet at its peak, but it was a work in progress.

Gradually, a network of routes came to criss-cross the whole region. Cultural and commercial exchanges multiplied. Increasingly complex hierarchies established themselves and Homo sapiens discovered the joys of administration. All this took extensive organization. To establish some degree of order, it was high time for our species to invent writing and enter history. Mathematics was to play a cutting-edge role in this nascent revolution.

Following the course of the Euphrates, we leave the northern plateaux that saw the birth of the first sedentary villages, and head towards the Sumer region that covers the plains of Lower Mesopotamia. It is here, in the southern steppes, that the chief population centres were then concentrated. Along the river we reach the towns of Kish, Nippur and Shuruppak. These towns were still young, but the centuries that lay ahead of them had grandeur and prosperity in store.