Mickael Launay - It All Adds Up

As I pass through the rooms of the Near Eastern Antiquities section, I am struck by the richness of the geometric patterns conceived by the Mesopotamians. Just as it was for our flint knapper’s biface, some symmetries are so ingenious that they must have been very thoughtfully designed in advance. The friezes running round the rims of these vases pique my interest.

The friezes are decorated bands with a single pattern repeated round the whole circumference of the pot. The most common ones include triangular sawtooth designs. There are also friezes showing two intertwined strings. Then there are friezes with angled rectangles, friezes with square indentations, friezes with pointed lozenges, with hatched triangles, with interlocking circles, and so on.

When one moves from one region to another or from one period to the next, trends can be seen. Certain patterns are very popular. They are reworked, transformed, improved in multiple variants. Then, several years later, they are essentially abandoned, replaced by other designs that are fashionable at the time.

My mathematician’s eyes light up as I spot symmetries, rotations and translations. Then in my mind I begin to sort and arrange all this. Several theorems from my undergraduate days come back to me. What I need is the classification of geometric transformations. I take out a notebook and a pencil and begin to scribble.

First, there are rotations. Appropriately, in front of me there is a frieze consisting of S-shaped patterns interlocking one after the other. I tilt my head to make sure I’m right. Yes, there’s no doubt, this one is invariant under a half-turn: if I were to take the earthenware jar and turn it upside down, the frieze would still look exactly the same.

Then there are symmetries. There are several types of these. I am gradually filling in my list and a treasure hunt begins. For each geometric transformation I look for the corresponding frieze. Moving from room to room, I retrace my steps. Some pieces are damaged, so I squint to try to reconstitute the patterns that ran across this clay thousands of years ago. When I find a new pattern, I tick it off. I look at the dates to try to reconstitute the chronology in which the patterns appeared.

How many patterns should I find in total? After a little thought, I finally manage to put my finger on this famous theorem. There are, in sum total, seven categories of friezes. Seven different groups of geometric transformations that can leave them invariant. Not one more, not one less.

That is not something the Mesopotamians knew. And with good reason, as the first formalization of the theory in question only began in the Renaissance. However, without knowing it, and without pretending to be doing anything other than decorating their pottery with harmonious and original designs, these prehistoric potters were actually undertaking the very first reasoning in a fantastic discipline, that would focus the efforts of a whole community of mathematicians thousands of years later.

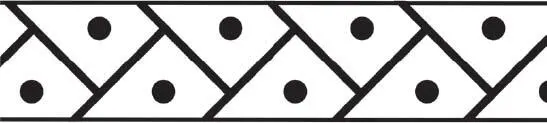
Looking over my notes, I see almost all the patterns. Almost? I’m still missing one of the seven friezes. This doesn’t surprise me a lot, as this frieze is clearly the most complicated one on the list. I am looking for a frieze that, if you flip it over horizontally, will have the same appearance but shifted by half a pattern length. Today, we call this a glide symmetry. This would have been a real challenge for Mesopotamians.

However, I still have not visited all the rooms, so I’m not losing hope – the hunt is still on. I observe the smallest detail, the least indication. Examples of the other six categories, those I have already observed, are piling up. In my notebook, the dates, sketches and other scribbles are getting muddled. But still no sign of the mysterious seventh frieze.

All at once, a rush of adrenalin. Behind this glass panel I have just spotted a piece that looks in a bit of a sorry state. A simple fragment. From top to bottom you can clearly make out four partial friezes, one above the other, and one of these has caught my eye. The third one down – it consists of what look like fragments of inclined interlocking rectangles. My eyes are blinking. I’m peering attentively, sketching the pattern quickly in my notebook, as though I’m afraid it will vanish before my eyes. It has the right geometry. This really is the glide symmetry. The seventh frieze is unmasked.

The caption next to it says: Fragment of beaker with horizontal décor of bands and pointed lozenges. Middle of the fifth millennium BC .

I insert it mentally in my chronology. Mid-fifth millennium BC. We are still in prehistory. More than a thousand years before the invention of writing – without knowing it – the Mesopotamian potters had listed all the cases of a theorem that would only be stated and proved 6,000 years later.

A few rooms further, I come across an earthenware jar with three handles, which also falls into the seventh category: even though the pattern has become a spiral, the geometric structure remains the same. A little further on again, there is another one. I would like to continue, but suddenly the décor changes and I have arrived at the end of the Near Eastern collection. If I continue, I will reach Greece. I cast a last glance at my notes; the friezes with glide symmetry can be counted on the fingers of one hand. I had a stroke of luck.

The first category is that of friezes that have no particular geometric property, and in which a simple pattern is repeated without symmetries or centres of rotation. This is, in particular, the case for friezes that are not based on geometric figures but on figurative drawings, for instance of animals.

The second category consists of friezes in which the horizontal line dividing the figure in two is an axis of symmetry.

The third category comprises friezes that have a vertical axis of symmetry. Since a frieze consists of a pattern that is repeated horizontally, the vertical axes of symmetry are also repeated.

The fourth category is that of friezes that are invariant under a rotation by a half-turn. Whether you look at these friezes from above or below you will always see the same thing.

The fifth category is that of glide symmetries. This notable category was the last one I discovered while passing through Mesopotamia. If you reflect such a frieze about a horizontal axis of symmetry (as per the second category) the frieze obtained is similar, but translated by half a pattern length.

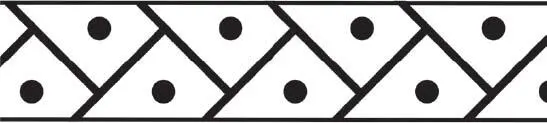
The sixth and seventh categories do not correspond to new geometric transformations, but combine several of the properties encountered in the previous categories. Thus, the friezes of the sixth category are those that have a horizontal symmetry, a vertical symmetry and a centre of rotation by a half-turn, all at the same time.