Mikhail Moklyachuk - Convex Optimization

THEOREM 1.8.– A function is lower semicontinuous on ℝ nif and only if for all a ∈ ℝ the set f –1(( a , +∞]) is open (or the complementary set f –1((–∞, a ]) is closed).

PROOF.– Let f be a lower semicontinuous on ℝ nfunction, let a ∈ ℝ and let ∈ f –1(( a , +∞]). Then there exists a δ -neighborhood of the point such that for all points x ∈ the inequality f ( x ) > a holds true. This means that . Consequently, the set f –1(( a , +∞]) is open.

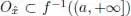Vice versa, if the set f –1(( a , +∞]) is open for any a ∈ ℝ and ∈ ℝ n, then and the function f is lower semicontinuous at point by agreement, or and ∈ f –1(( a , +∞]), when . Since the set f –1(( a , +∞]) is open, then there exists a δ -neighborhood of the point such that and f ( x ) > a for all x ∈ . Consequently, the function f is lower semicontinuous at point . □

THEOREM 1.9.– ( Weierstrass theorem ) A lower (upper) semicontinuous on a non-empty bounded closed subset X of the space ℝ nfunction is bounded from below (from above) on X and attains the smallest (largest) value.

THEOREM 1.10.– ( Weierstrass theorem ) If a function f ( x ) is lower semicontinuous and for some number a the set { x : f ( x ) ≤ a } is non-empty and bounded, then the function f ( x ) attains its absolute minimum.

COROLLARY 1.1.– If a function f ( x ) is lower (upper) semicontinuous on ℝ nand

then the function f ( x ) attains its minimum (maximum) on each closed subset of the space ℝ n.

THEOREM 1.11.– ( Necessary conditions of the first order ) If is a point of local extremum of the differentiable at the point function f ( x ), then all partial derivatives of the function f ( x ) are equal to zero at the point :

THEOREM 1.12.– ( Necessary conditions of the second order ) If is a point of local minimum of the function f ( x )>, which has the second-order partial derivatives at the point , then the following condition holds true:

This condition means that the matrix

is non-negative definite.

THEOREM 1.13.– ( Sufficient conditions of the second order ) Let a function have the second-order partial derivatives at a point and let the following conditions hold true:

Then is the point of local minimum of the function f ( x ).

The second condition of the theorem means that the matrix

is positive definite.

THEOREM 1.14.– ( Sylvester’s criterion ) A matrix A is positive definite if and only if its principal minors are positive. A matrix A is negative definite if and only if (–1) kdet Ak > 0, where