
In other words, if  ∈ locmin (locmax), then there exists a neighborhood
∈ locmin (locmax), then there exists a neighborhood  of the point
of the point  such that
such that

in the problem
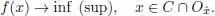
The theory of extremum problems gives general rules for solving extremum problems. The theory of necessary conditions of the extremum is more developed. The necessary conditions of the extremum make it possible to allocate a set of points among which solutions of the problem are situated. Such a set is called a critical set, and the points themselves are called critical points. As a rule, a critical set does not contain many points and a solution of the problem can be found by one or another method.
1.2. Optimization problems with objective functions of one variable
Let f : ℝ → ℝ be a function of one real variable.
DEFINITION 1.1.– A function f is said to be lower semicontinuous (upper semicontinuous) at a point if for every ε > 0, there exists a δ > 0 such that the inequality

holds true for all x ∈ (  ,
, 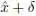 ).
).
DEFINITION 1.2.– (Equivalent) A function f is said to be lower semicontinuous (upper semicontinuous) at a point  if for every a ∈ ℝ,
if for every a ∈ ℝ,  there exists δ > 0, such that the inequality
there exists δ > 0, such that the inequality

holds true for all x ∈ (  ,
, 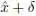 ).
).
If the function takes values in  , then definitions 1.1 and 1.2 make sense when
, then definitions 1.1 and 1.2 make sense when  . In the case where
. In the case where  , the function f is considered to be lower semicontinuous ( upper semicontinuous ) by agreement.
, the function f is considered to be lower semicontinuous ( upper semicontinuous ) by agreement.
Here are examples of semicontinuous functions:
1 1) the function y = [x] (integer part of x) is upper semicontinuous at the points of discontinuity;
2 2) the function y = {x} (fractional part of x) is lower semicontinuous at the points of discontinuity;
3 3) the Dirichlet function, which is equal to 0 at rational points and equal to 1 at irrational points, is lower semicontinuous at each rational point and upper semicontinuous at each irrational point;
4 4) if the function has a local minimum (maximum) at the point then it is lower (upper) semicontinuous at the point;
5 5) the function A for x ≠ 0, f(0) = +∞, is lower semicontinuous at the point 0. If we define the function at the point 0 arbitrarily, then it will remain lower semicontinuous.
THEOREM 1.1.– Let f and g be lower semicontinuous functions. Then:
– the function f + g is lower semicontinuous;
– the function αf is lower semicontinuous for α ≥ 0 and it is upper semicontinuous for α ≤ 0;
– the function f · g is lower semicontinuous for f ≥ 0, g ≥ 0;
– the function 1/f is upper semicontinuous if f > 0;
– the function max{f, g}, min{f, g} is lower semicontinuous;
– the functions sup{fi} (inf{fi}) are lower (upper) semicontinuous, if the functions fi are lower (upper) semicontinuous.
THEOREM 1.2.– ( Weierstrass theorem ) A lower (upper) semicontinuous on the interval [ a , b ] function f : ℝ → ℝ is bounded from below (from above) on [ a , b ] and attains the smallest (largest) value.
THEOREM 1.3.– ( Fermat’s theorem ) If  is a point of local extremum of the differentiable at the point
is a point of local extremum of the differentiable at the point  function f ( x ), then
function f ( x ), then  .
.
Fermat’s theorem gives the first-order necessary condition for existence of a local extremum of the function f ( x ) at point  . The following theorems give the second-order necessary and sufficient conditions for the extremum.
. The following theorems give the second-order necessary and sufficient conditions for the extremum.
THEOREM 1.4.– ( Necessary conditions of the second order ) If  is a point of local minimum (maximum) of the function f ( x ), which has the second-order derivative at the point
is a point of local minimum (maximum) of the function f ( x ), which has the second-order derivative at the point  then the following conditions hold true:
then the following conditions hold true:

THEOREM 1.5.– ( Sufficient conditions of the second order ) If the function f ( x ) has at a point  the second-order derivative and
the second-order derivative and
Читать дальше


 ∈ locmin (locmax), then there exists a neighborhood
∈ locmin (locmax), then there exists a neighborhood  of the point
of the point 
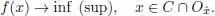

 ,
, 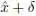 ).
). there exists δ > 0, such that the inequality
there exists δ > 0, such that the inequality
 , then definitions 1.1 and 1.2 make sense when
, then definitions 1.1 and 1.2 make sense when  . In the case where
. In the case where  , the function f is considered to be lower semicontinuous ( upper semicontinuous ) by agreement.
, the function f is considered to be lower semicontinuous ( upper semicontinuous ) by agreement. .
.











