Convex analysis and optimization have an increasing impact on many areas of mathematics and applications including control systems, estimation and signal processing, communications and networks, electronic circuit design, data analysis and modeling, statistics, and economics and finance. There are several fundamental books devoted to different aspects of convex analysis and optimization. Among them we can mention Optima and Equilibria: An Introduction to Nonlinear Analysis by Aubin (1998), Convex Analysis by Rockafellar (1970), Convex Analysis and Minimization Algorithms (in two volumes) by Hiriart-Urruty and Lemaréchal (1993) and its abridged version (2002), Convex Analysis and Nonlinear Optimization by Borwein and Lewis (2000), Convex Optimization by Boyd and Vandenberghe (2004), Convex Analysis and Optimization by Bertsekas et al . (2003), Convex Analysis and Extremal Problems by Pshenichnyj (1980), A Course in Optimization Methods by Sukharev et al . (2005), Convex Analysis: An Introductory Text by Van Tiel (1984), as well as other books listed in the bibliography (see Alekseev et al . (1984, 1987); Alekseev and Timokhov (1991); Clarke (1983); Hiriart-Urruty (1998); Ioffe and Tikhomirov (1979) and Nesterov (2004)).
This book provides easy access to the basic principles and methods for solving constrained and unconstrained convex optimization problems. Structurally, the book has been divided into the following parts: basic methods for solving constrained and unconstrained optimization problems with differentiable objective functions, convex sets and their properties, convex functions, their properties and generalizations, subgradients and subdifferentials, and basic principles and methods for solving constrained and unconstrained convex optimization problems. The first part of the book describes methods for finding the extremum of functions of one and many variables. Problems of constrained and unconstrained optimization (problems with restrictions of inequality and inequality types) are investigated. The necessary and sufficient conditions of the extremum, the Lagrange method, are described.
The second part is the most voluminous in terms of the amount of material presented. Properties of convex sets and convex functions directly related to extreme problems are described. The basic principles of subdifferential calculus are outlined. The third part is devoted to the problems of mathematical programming. The problem of convex programming is considered in detail. The Kuhn–Tucker theorem is proved and the economic interpretations of the Kuhn–Tucker vector are described.
We give detailed proofs for most of the results presented in the book and also include many figures and exercises for better understanding of the material. Finally, we present solutions and hints to selected exercises at the end of the book. Exercises are given at the end of each chapter while figures and examples are provided throughout the whole text. The list of references contains texts which are closely related to the topics considered in the book and may be helpful to the reader for advanced studies of convex analysis, its applications and further extensions. Since only elementary knowledge in linear algebra and basic calculus is required, this book can be used as a textbook for both undergraduate and graduate level courses in convex optimization and its applications. In fact, the author has used these lecture notes for teaching such classes at Kyiv National University. We hope that the book will make convex optimization methods more accessible to large groups of undergraduate and graduate students, researchers in different disciplines and practitioners. The idea was to prepare materials of lectures in accordance with the suggestion made by Einstein: “Everything should be made as simple as possible, but not simpler.”
1
Optimization Problems with Differentiable Objective Functions
1.1. Basic concepts
The word “maximum” means the largest, and the word “minimum” means the smallest. These two concepts are combined with the term “extremum”, which means the extreme. Also pertinent is the term “optimal” (from Latin optimus ), which means the best. The problems of determining the largest and smallest quantities are called extremum problems . Such problems arise in different areas of activity and therefore different terms are used for the descriptions of the problems. To use the theory of extremum problems, it is necessary to describe problems in the language of mathematics. This process is called the formalization of the problem.
The formalized problem consists of the following elements:
– objective function ;
– domain X of the definition of the objective functional f;
– constraint: C ⊂ X.
Here,  is an extended real line, that is, the set of all real numbers, supplemented by the values +∞ and –∞, C is a subset of the domain of definition of the objective functional f . So to formalize an optimization problem means to clearly define and describe elements f , C and X . The formalized problem is written in the form
is an extended real line, that is, the set of all real numbers, supplemented by the values +∞ and –∞, C is a subset of the domain of definition of the objective functional f . So to formalize an optimization problem means to clearly define and describe elements f , C and X . The formalized problem is written in the form
[1.1] 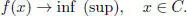
Points of the set C are called admissible points of the problem [1.1]. If C = X , then all points of the domain of definition of the function are admissible. The problem [1.1]in this case is called a problem without constraints .
The maximization problem can always be reduced to the minimization problem by replacing the functional f with the functional g = – f . And, on the contrary, the minimization problem in the same way can be reduced to the maximization problem. If the necessary conditions for the extremum in the minimization problem and maximization problem are different, then we write these conditions only for the minimization problem. If it is necessary to investigate both problems, then we write down

An admissible point  is a point of absolute or global minimum ( maximum ) of the extremum problem if for any x . ∈ C the inequality holds true
is a point of absolute or global minimum ( maximum ) of the extremum problem if for any x . ∈ C the inequality holds true
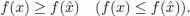
Then we write  ∈ absmin (absmax). The point of the absolute minimum (maximum) is called a solution of the problem . The value
∈ absmin (absmax). The point of the absolute minimum (maximum) is called a solution of the problem . The value 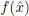 , where
, where  is a solution of the problem, is called a numerical value of the problem. This value is denoted by S min( S max).
is a solution of the problem, is called a numerical value of the problem. This value is denoted by S min( S max).
In addition to global extremum problems, local extremum problems are also studied. Let X be a normed space. A local minimum ( maximum ) of the problem is reached at a point  that is
that is  ∈ locmin (locmax), if
∈ locmin (locmax), if  ∈ C and there exists a number δ > 0 such that for any admissible point x ∈ C that satisfies condition
∈ C and there exists a number δ > 0 such that for any admissible point x ∈ C that satisfies condition 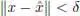 , the inequality holds true
, the inequality holds true
Читать дальше

 is an extended real line, that is, the set of all real numbers, supplemented by the values +∞ and –∞, C is a subset of the domain of definition of the objective functional f . So to formalize an optimization problem means to clearly define and describe elements f , C and X . The formalized problem is written in the form
is an extended real line, that is, the set of all real numbers, supplemented by the values +∞ and –∞, C is a subset of the domain of definition of the objective functional f . So to formalize an optimization problem means to clearly define and describe elements f , C and X . The formalized problem is written in the form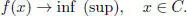

 is a point of absolute or global minimum ( maximum ) of the extremum problem if for any x . ∈ C the inequality holds true
is a point of absolute or global minimum ( maximum ) of the extremum problem if for any x . ∈ C the inequality holds true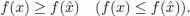
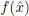 , where
, where 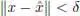 , the inequality holds true
, the inequality holds true










