First published 2020 in Great Britain and the United States by ISTE Ltd and John Wiley & Sons, Inc.
Apart from any fair dealing for the purposes of research or private study, or criticism or review, as permitted under the Copyright, Designs and Patents Act 1988, this publication may only be reproduced, stored or transmitted, in any form or by any means, with the prior permission in writing of the publishers, or in the case of reprographic reproduction in accordance with the terms and licenses issued by the CLA. Enquiries concerning reproduction outside these terms should be sent to the publishers at the undermentioned address:
John Wiley & Sons, Inc.
The rights of Mikhail Moklyachuk to be identified as the author of this work have been asserted by him in accordance with the Copyright, Designs and Patents Act 1988.
| ℕ |
Set of natural numbers |
| ℤ |
Set of integer numbers |
| ℤ + |
Set of non-negative integer numbers |
| ℝ |
Set of real numbers |
 |
Extended set of real numbers |
| ℚ |
Set of rational numbers |
| ℝ n |
Set of real n -vectors |
| ℝ m × n |
Set of real m × n -matrices |
| ℝ + |
Set of non-negative real numbers |
| ℝ ++ |
Set of positive real numbers |
| ℂ |
Set of complex numbers |
| ℂ n |
Set of complex n-vectors |
| ℂ m × n |
Set of complex m × n -matrices |
 |
Set of symmetric n × n -matrices |
 |
Set of symmetric positive semidefinite n × n -matrices |
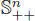 |
Set of symmetric positive definite n × n -matrices |
 |
Identity matrix |
| X ⊤ |
Transpose of matrix X |
| tr ( X ) |
Trace of matrix X |
| λ i( X ) |
i th largest eigenvalue of symmetric matrix X |
| 〈· , ·〉 |
Inner product |
| x ⊥ y |
Vectors x and y are orthogonal: 〈 x , y 〉 = 0 |
| V ⊥ |
Orthogonal complement of subspace V |
| diag( X ) |
Diagonal matrix with diagonal entries x 1, … , xn |
| rank ( X ) |
Rank of matrix X |
| ‖·‖ |
A norm |
| ‖·‖ * |
Dual of norm ‖·‖ |
| ‖ x ‖ 2 |
Euclidean norm of vector x |
| x ⪯ y |
Componentwise inequality between vectors x and y |
| x ≺ y |
Strict componentwise inequality between vectors x and y |
| X ⪯ Y |
Matrix inequality between symmetric matrices X and Y |
| X ≺ Y |
Strict matrix inequality between symmetric matrices X and Y |
| X ⪯ K Y |
Generalized inequality induced by proper cone K |
| X ≺ K Y |
Strict generalized inequality induced by proper cone K |
| int X |
Interior of set X |
| ri X |
Relative interior of set X |
| conv X |
Convex hull of set X |
| aff X |
Affine hull of set X |
| cone X |
Conic hull of set X |
| Lin X |
Linear hull of set X |
 |
Closure of set X |
 |
Closed convex hull of set X |
| dim X |
Dimension of set X |
| ∂ X |
Boundary of set X |
| K * |
Dual cone associated with cone K |
 |
A ray proceeding from a point 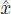 in the direction h in the direction h |
| Hpβ |
A hyperplane with the normal vector p |
 |
Half-spaces generated by hyperplane Hpβ |
| π X( a ) |
Projection of point a onto set X |
| ρ ( X 1, X 2) |
Distance between sets X 1and X 2 |
| epi f |
Epigraph of function f |
| Sr ( f ) |
Sublevel set of function f |
| dom f |
Effective set of function f |
| f 1⊕ f 2 |
Infimal convolution of functions f 1, f 2 |
| μ ( x \ X ) |
Minkowski function |
| γX ( x ) |
Gauge function |
| δ ( x \ X ) |
Indicator function |
| σ ( x \ X ) |
Support function |
| f * |
Conjugate function |
| ∂f ( x ) |
Subdifferential of function f at point x |
 |
Superdifferential of function f at point x |
| ∏(ℝ m) |
Set of all non-empty subsets of the space ℝ m |





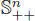




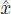 in the direction h
in the direction h












