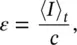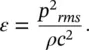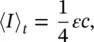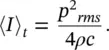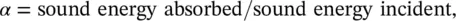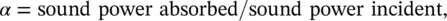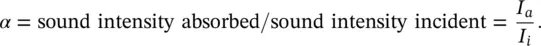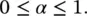Malcolm J. Crocker - Engineering Acoustics

In enclosed spaces the wave acoustics approach is useful, particularly if the enclosed volume is small and simple in shape and the boundary conditions are well defined. In the case of rigid walls of simple geometry, the wave equation is used, and after the applicable boundary conditions are applied, the solutions for the natural (eigen) frequencies for the modes (standing waves) are found. See Refs. [23, 24], and chapter 6 in the Handbook of Acoustics [1] for more details. However, for large rooms with irregular shape and absorbing boundaries, the wave approach becomes impracticable and other approaches must be sought. The ray acoustics approach together with the multiple‐image‐source concept is useful in some room problems, particularly in auditorium design or in factory spaces where barriers are involved. However, in many cases a statistical approach where the energy in the sound field is considered is the most useful. See Refs. [25, 26] and also chapters 60–62 in the Handbook of Acoustics [1] for more detailed discussion of this approach. Some of the fundamental concepts are briefly described here.

For a plane wave progressing in one direction in a duct of unit cross‐section area, all of the sound energy in a column of fluid c metres in length must pass through the cross‐section in one second. Since the intensity 〈 I 〉 tis given by p 2 rms /ρc , then the total sound energy in the fluid column c metres long must also be equal to 〈 I 〉 t. The energy per unit volume ε (joules per cubic metre) is thus

(3.69)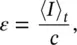

or

(3.70)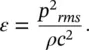

The energy density ε may be derived by alternative means and is found to be the same as that given in Eq. (3.69)in most acoustic fields, except very close to sources of sound and in standing‐wave fields. In a room with negligibly small absorption in the air or at the boundaries, the sound field created by a source producing broadband sound will become very reverberant (the sound waves will reach a point with equal probability from any direction). In addition, for such a case the sound energy may be said to be diffuse if the energy density is the same anywhere in the room. For these conditions, the time‐averaged intensity incident on the walls (or on an imaginary surface from one side) is

(3.71)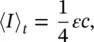

or

(3.72)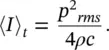

In any real room, the walls will absorb some sound energy (and convert it into heat).

Near to a source, we call the sound field, the near acoustic field . Far from the source, we call the field the far acoustic field . The extent of the near field depends on:

1 The type of source: (monopole, dipole, size of machine, type of machine, etc.)

2 Frequency of the sound.

In the near field of a source, the sound pressure and particle velocity tend to be very nearly out of phase (≈90°).

In the far field , the sound pressure and particle velocity are very nearly in phase. Note, far from any source, the sound wave fronts flatten out in curvature, and the waves appear to an observer to be like plane waves. In‐plane progressive waves, the sound pressure and particle velocity are in phase (provided there are no reflected waves). Thus far from a source (or in a plane progressive wave) p/u = ρc . Note ρc is a real number, so the sound pressure p and particle velocity u must be in phase.

Figure 3.17shows the example of a finite monopole source with a normal simple harmonic velocity amplitude U . On the surface of the monopole, the surface velocity is equal to the particle velocity. The particle velocity decreases in inverse proportion to the distance from the source center O .

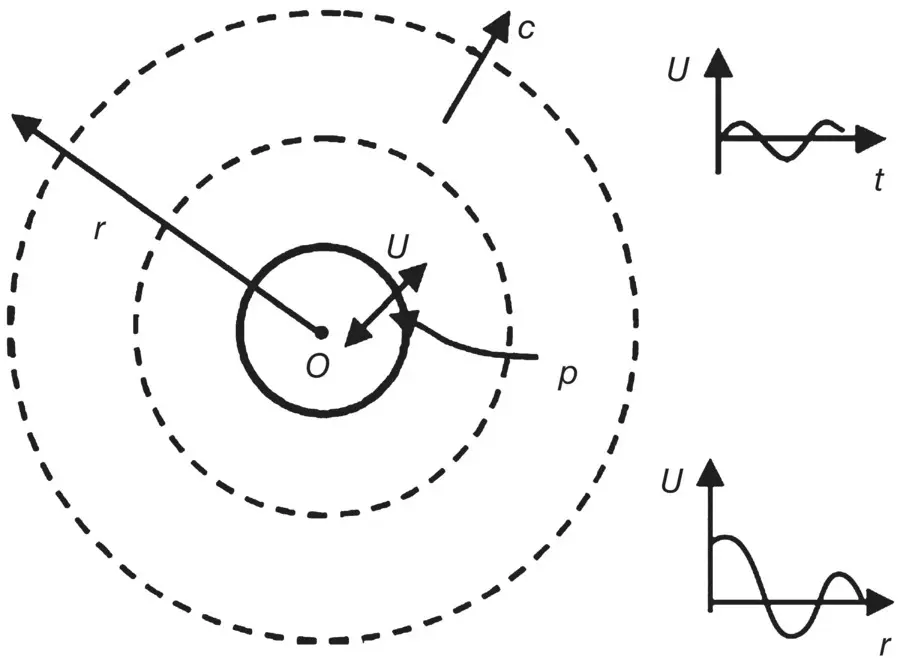
Figure 3.17 Example of monopole. On the monopole surface, velocity of surface U = particle velocity in the fluid.

It is common to make the assumption that kr = 2 πf r/c = 10 is the boundary between the near and far fields. Note this is only one criterion and that there is no sharp boundary, but only a gradual transition. First we should also think of the type and the dimensions of the source and assume, say that r ≫ d , where d is a source dimension. We might say that r > 10 d should also be applied as a secondary criterion to determine when we are in the far field.

In a confined space there will be reflections, and far from the source the reflections will dominate. We call this reflection‐dominated region the reverberant field . The region where reflections are unimportant and where a doubling of distance results in a sound pressure drop of 6 dB is called the free or direct field (see Figure 3.18).

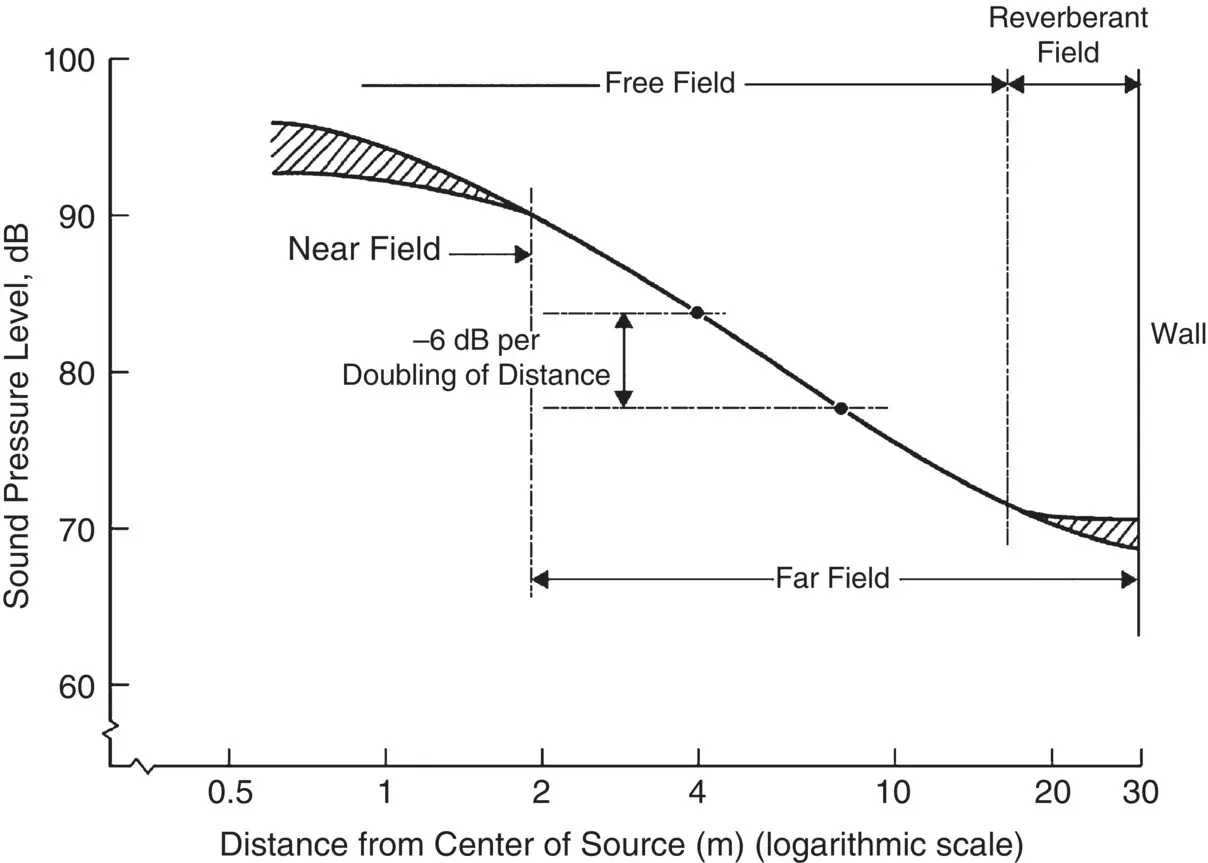
Figure 3.18 Sound pressure level in an interior sound field.

The sound absorption coefficient α of sound‐absorbing materials (curtains, drapes, carpets, clothes, fiberglass, acoustical foams, etc.), is defined as

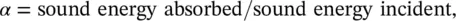
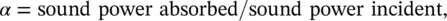
(3.73)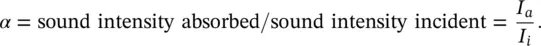

Note that α also depends on the angle of incidence. The absorption coefficient of materials depends on frequency as well. Thicker materials absorb more sound energy (particularly important at low frequency). See Figure 3.19.

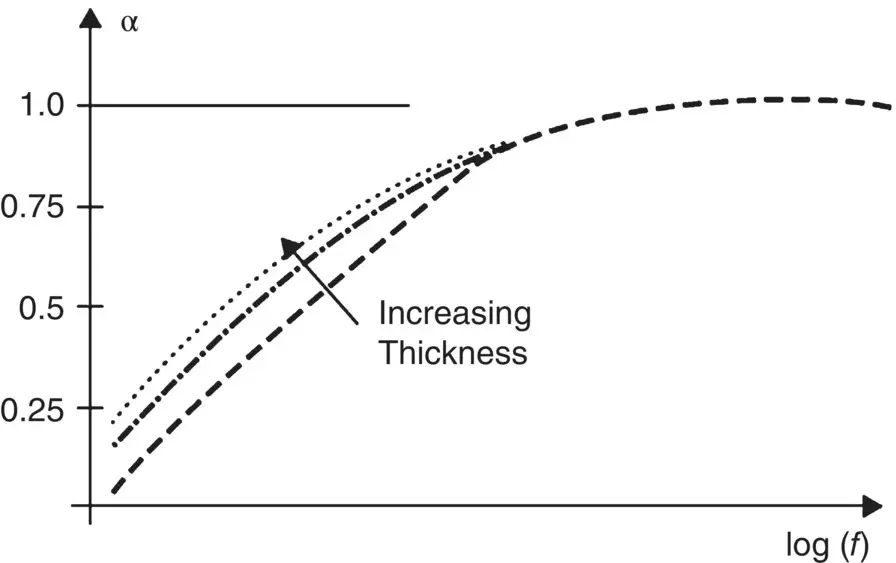
Figure 3.19 Sound absorption coefficient α of typical absorbing materials as a function of frequency.

If all the sound energy is absorbed, α = 1 (none reflected). If no sound energy is absorbed, α = 0:

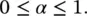
If α = 1, the sound absorption is perfect (e.g. an open window).

The behavior of sound‐absorbing materials is described in more detail in Chapter 9of this book.