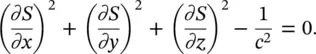Malcolm J. Crocker - Engineering Acoustics

A plane sound wave in air is incident normally on a boundary between air and water. If each medium can be assumed to be infinite in extent, compute the energy reflection and transmission coefficients.

At standard temperature and atmospheric pressure we have that in water ρ = 998 kg/m 3and c = 1480 m/s. Then, the characteristic impedance of water is ρc = 1 480 000 rayls.

Then, R = [(415–1 480 000)/(415 + 1 480 000)] 2= 0.999 and

T = 4(415)(1 480 000)/(415 + 1 480 000) 2= 0.001, or simply T = 1– R = 0.001. Therefore, when a sound wave passes from air to water most of its energy is reflected back because of the impedance offered by the liquid medium.

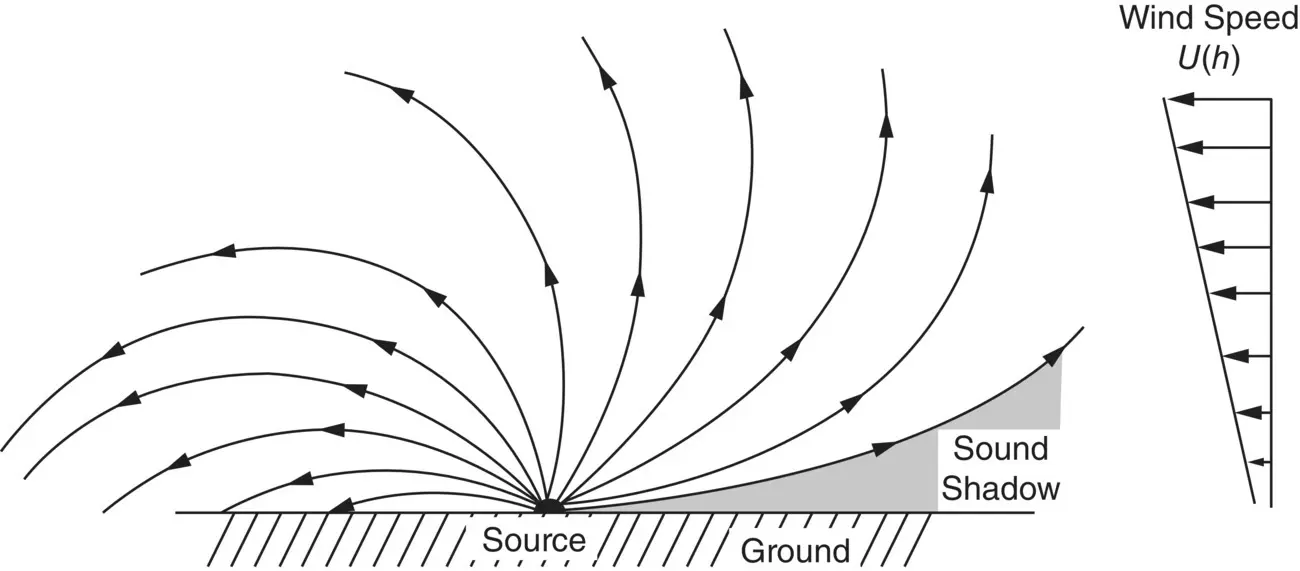
Figure 3.14 Refraction of sound in air with wind speed U ( h ) increasing with altitude h .

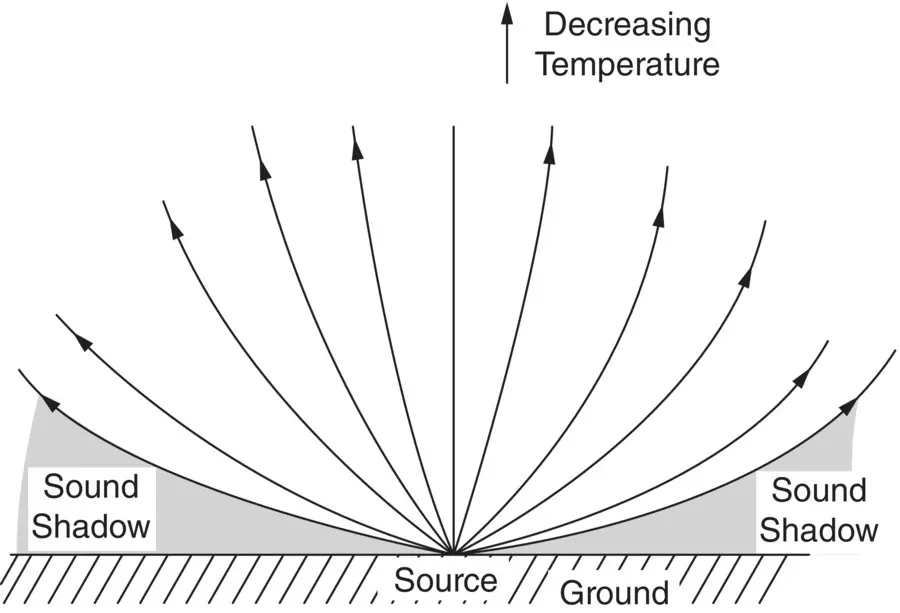
Figure 3.15 Refraction of sound in air with normal temperature lapse (temperature decreases with altitude).

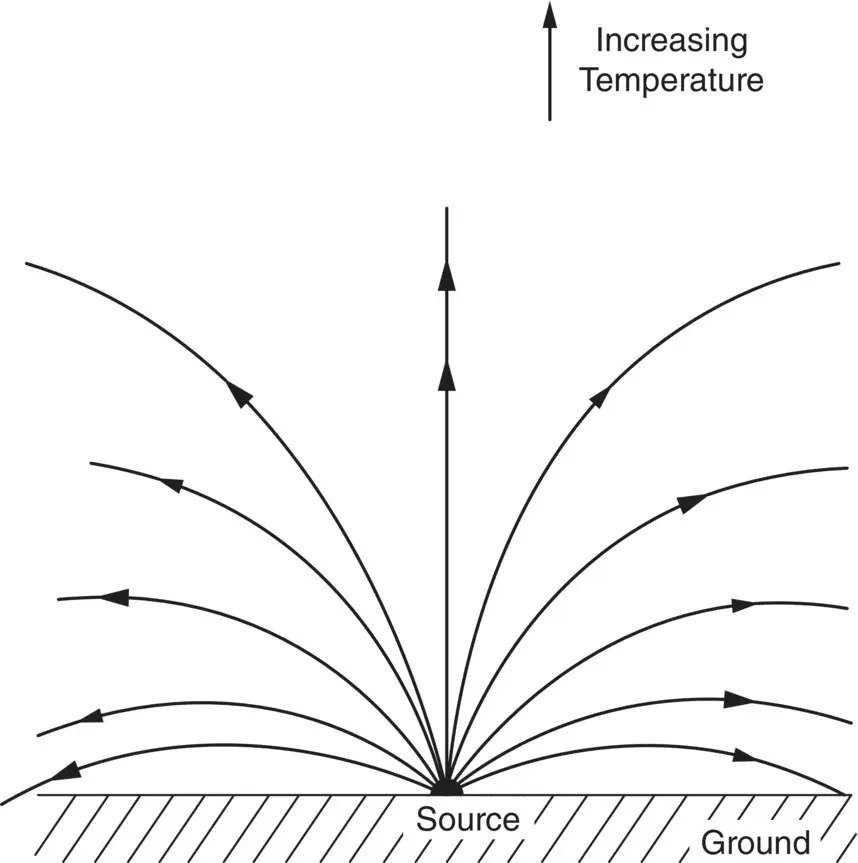
Figure 3.16 Refraction of sound in air with temperature inversion.

As discussed before, when the characteristic impedance ρc of a fluid medium changes, incident sound waves are both reflected and transmitted. It can be shown that if a plane sound wave is incident at an oblique angle on a plane boundary between two fluids, then the wave transmitted into the changed medium changes direction. This effect is called refraction . Temperature changes and wind speed changes in the atmosphere are important causes of refraction.

Wind speed normally increases with altitude, and Figure 3.14shows the refraction effects to be expected for an idealized wind speed profile. Atmospheric temperature changes alter the speed of sound c , and temperature gradients can also produce sound shadow and focusing effects, as seen in Figures 3.15and 3.16.

When a sound wave meets an obstacle, some of the sound wave is deflected. The scattered wave is defined to be the difference between the resulting wave with the obstacle and the undisturbed wave without the presence of the obstacle. The scattered wave spreads out in all directions interfering with the undisturbed wave. If the obstacle is very small compared with the wavelength, no sharp‐edged sound shadow is created behind the obstacle. If the obstacle is large compared with the wavelength, it is normal to say that the sound wave is reflected (in front) and diffracted (behind) the obstacle (rather than scattered ).

In this case when the obstacle is large a strong sound shadow is caused in which the wave pressure amplitude is very small. In the zone between the sound shadow and the region fully “illuminated” by the source, the sound wave pressure amplitude oscillates. These oscillations are maximum near the shadow boundary and minimum well inside the shadow. These oscillations in amplitude are normally termed diffraction bands . One of the most common examples of diffraction caused by a body is the diffraction of sound over the sharp edge of a barrier or screen . For a plane homogeneous sound wave it is found that a strong shadow is caused by high‐frequency waves, where h/λ ≥ 1 and a weak shadow where h/λ ≤ 1, where h is the barrier height and λ is the wavelength. For intermediate cases where h/λ ≈ 1, a variety of interference and diffraction effects are caused by the barrier.

Scattering is caused not only by obstacles placed in the wave field but also by fluid regions where the properties of the medium such as its density or compressibility change their values from the rest of the medium. Scattering is also caused by turbulence (see chapters 5 and 28 in the Handbook of Acoustics [1]) and from rain or fog particles in the atmosphere and bubbles in water and by rough or absorbent areas on wall surfaces.

There are three main modeling approaches in acoustics, which may be termed wave acoustics, ray acoustics, and energy acoustics. So far in this chapter we have mostly used the wave acoustics approach in which the acoustical quantities are completely defined as functions of space and time. This approach is practical in certain cases where the fluid medium is bounded and in cases where the fluid is unbounded as long as the fluid is homogenous. However, if the fluid properties vary in space due to variations in temperature or due to wind gradients, then the wave approach becomes more difficult and other simplified approaches such as the ray acoustics approach described here and in chapter 3 of the Handbook of Acoustics [1] are useful. This approach can also be extended to propagation in fluid‐submerged elastic structures, as described in chapter 4 of the Handbook of Acoustics [1]. The energy approach is described in Section 3.13.

In the ray acoustics approach, rays are obtained that are solutions to the simplified eikonal equation ( Eq. (3.68))

(3.68)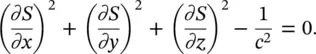

The ray solutions can provide good approximations to more exact acoustical solutions. In certain cases they also satisfy the wave equation [14]. The eikonal S ( x , y , z ) represents a surface of constant phase (or wavefront) that propagates at the speed of sound c . It can be shown that Eq. (3.68)is consistent with the wave equation only in the case when the frequency is very high [7]. However, in practice, it is useful, provided the changes in the speed of sound c are small when measured over distances comparable with the wavelength. In the case where the fluid is homogeneous (constant sound speed c and density ρ throughout), S is a constant and represents a plane surface given by S = ( αx + βy + γz ) /c , where α , β , and γ are the direction cosines of a straight line (a ray) that is perpendicular to the wavefront (surface S ). If the fluid can no longer be assumed to be homogeneous and the speed of sound c ( x , y , z ) varies with position, the approach becomes approximate only. In this case some paths bend and are no longer straight lines. In cases where the fluid has a mean flow, the rays are no longer quite parallel to the normal to the wavefront. This ray approach is described in more detail in several books [6, 12, 15, 16] and in chapter 3 of the Handbook of Acoustics [1] (where in this chapter the main example is from underwater acoustics).

The ray approach is also useful for the study of propagation in the atmosphere and is a method to obtain the results given in Figures 3.14– 3.16. It is observed in these figures that the rays always bend in a direction toward the region where the sound speed is less. The effects of wind gradients are somewhat different since in that case the refraction of the sound rays depends on the relative directions of the sound rays and the wind in each fluid region.