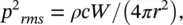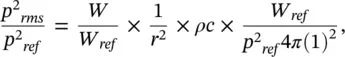(3.45) 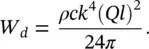
The dipole is obviously a much less efficient radiator than a monopole, particularly at low frequency.
Two monopoles of equal sound power W = 0.1 watt at 150 Hz, but pulsating with a phase difference of 180° are spaced λ /12 apart. Determine the sound power of this dipole at 150 Hz.
We know that l = λ /12, λ = 343/150 = 2.29 m, and W m= 0.1 watt. If we compare the sound power of a dipole W dwith that of a monopole W m( Eqs. (3.44)and (3.45)) we find that
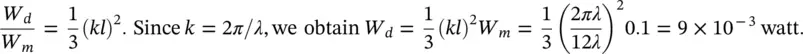
Therefore, the sound power radiated by the dipole is 9 mW.
In practical situations with real directional sound sources and where background noise and reflections are important, use of Eq. (3.43)becomes difficult and less accurate, and then the sound power is more conveniently determined from Eq. (3.41)with a sound intensity measurement system. See Ref. [22] in this book and chapter 106 in the Handbook of Acoustics [1].
We note that since p/u r= ρc (where ρ = mean air density kg/m 3and c = speed of sound 343 m/s) for a plane wave or sufficiently far from any source, that
(3.46) 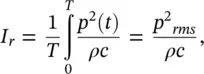
where Eq. (3.46)is true for random noise as well as for a single‐frequency sound, known as a pure tone.
Note that for such cases we only need to measure the mean‐square sound pressure with a simple sound level meter (or at least a simple measurement system) to obtain the sound intensity from Eq. (3.46)and then from that the sound power W watts from Eq. (3.41)is
(3.47) 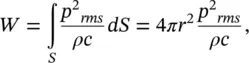
for an omnidirectional source (monopole) with no reflections and no background noise. This result is true for noise signals and pure tones that are produced by omnidirectional sources and in the so‐called far acoustic field.
For the special case of a pure‐tone (single‐frequency) source of sound pressure amplitude, 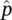 , we note that
, we note that 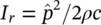 and
and 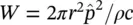 from Eq. (3.47).
from Eq. (3.47).
For measurements on a hemisphere, W = 2 πr 2 p 2 rms /ρc and for a pure‐tone source 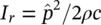 , and
, and 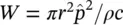 , from Eq. (3.47).
, from Eq. (3.47).
Note that in the general case, the source is not omnidirectional, or more importantly, we must often measure quite close to the source so that we are in the near acoustic field, not the far acoustic field. However, if appreciable reflections or background noise (i.e. other sound sources) are present, then we must measure the intensity I rin Eq. (3.41). Figure 3.8shows two different enclosing surfaces that can be used to determine the sound power of a source. The sound intensity I nmust always be measured perpendicular (or normal) to the enclosing surfaces used. Measurements are normally made with a two‐microphone probe (see Ref. [22]). The most common microphone arrangement is the face‐to‐face model (see Figure 3.9).
The microphone arrangement shown also indicates the microphone separation distance, Δ r , needed for the intensity calculations [22]. In the face‐to‐face arrangement a solid cylindrical spacer is often put between the two microphones to improve the performance.
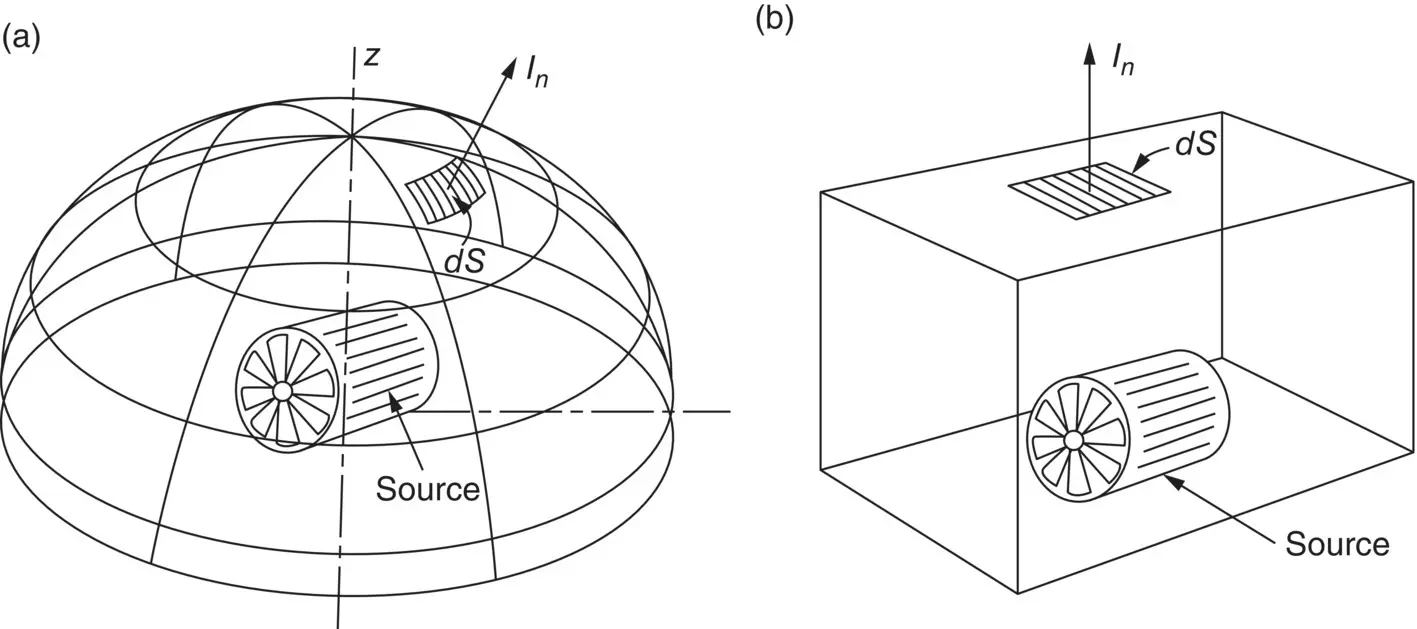
Figure 3.8 Sound intensity I n, being measured on (a) segment dS of an imaginary hemispherical enclosure surface and (b) an elemental area dS of a rectangular enclosure surface surrounding a source having a sound power W .
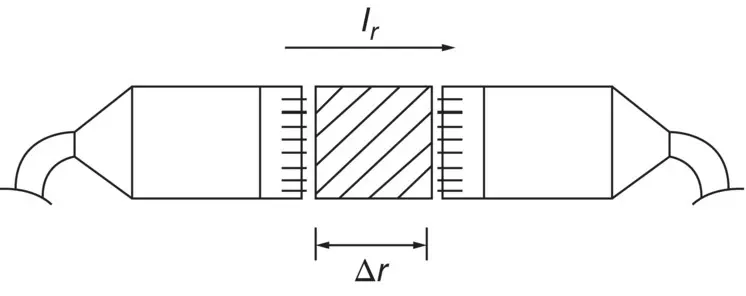
Figure 3.9 Sound intensity probe microphone arrangement commonly used.
By making measurements around a source (an engine exhaust pipe) it is found that it is largely omnidirectional at low frequency (in the range of 50–200 Hz). If the measured sound pressure level on a spherical surface 10 m from the source is 60 dB at 100 Hz, which is equivalent to a mean‐square sound pressure p 2 rmsof (20 × 10 −3) 2(Pa) 2, what is the sound power in watts at 100 Hz frequency?
Assuming that ρ = 1.21 kg/m 3and c = 343 m/s, so ρc = 415 ≈ 400 rayls:
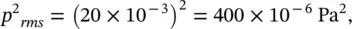
then from Eq. (3.47):
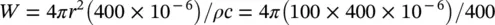
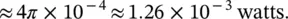
If the sound intensity level, measured using a sound intensity probe at the same frequency, as in Example 3.8, but at 1 m from the exhaust exit, is 80 dB (which is equivalent to 0.0001 W/m 2), what is the sound power of the exhaust source at this frequency?
From Eq. (3.41) 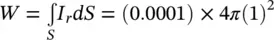 (for an omnidirectional source). Then W = 1.26 × 10 −3watts (the same result as Example 3.8).
(for an omnidirectional source). Then W = 1.26 × 10 −3watts (the same result as Example 3.8).
Sound intensity measurements do and should give the same result as sound pressure measurements made in a free field.
Far away from omnidirectional sound sources, provided there is no background noise and reflections can be ignored:
(3.48) 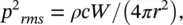
(3.49) 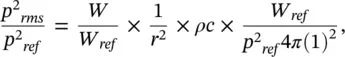
Читать дальше

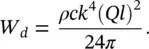
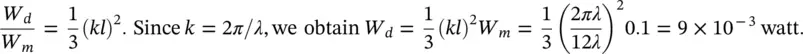
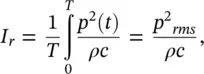
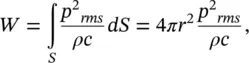
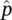 , we note that
, we note that 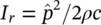 and
and 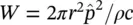 from Eq. (3.47).
from Eq. (3.47).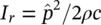 , and
, and 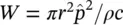 , from Eq. (3.47).
, from Eq. (3.47).

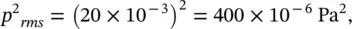
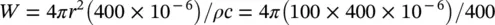
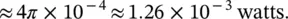
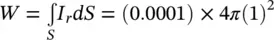 (for an omnidirectional source). Then W = 1.26 × 10 −3watts (the same result as Example 3.8).
(for an omnidirectional source). Then W = 1.26 × 10 −3watts (the same result as Example 3.8).