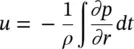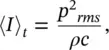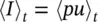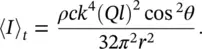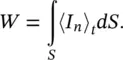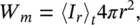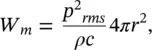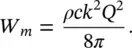The sound pressure of a dipole source has near‐field and far‐field regions that exhibit similar behaviors to the particle velocity near‐field and far‐field regions of a monopole.
Close to the source (the near field), for some fixed angle θ , the sound pressure falls off rapidly, p ∝ 1 /r 2, while far from the source (the far field kr ≥ 1), the pressure falls off more slowly, p ∝ 1 /r . In the near field, the sound pressure level decreases by 12 dB for each doubling of distance r . In the far field the decrease in sound pressure level is only 6 dB for doubling of r (like a monopole). The phase of the sound pressure also changes with distance r , since close to the source the sine term dominates and far from the source the cosine term dominates. The particle velocity may be obtained from the sound pressure ( Eq. (3.36)) and use of Euler's equation (see Eq. (3.37)). It has an even more complicated behavior with distance r than the sound pressure, having three distinct regions.
An oscillating force applied at a point in space gives rise to results identical to Eq. (3.36), and hence there are many real sources of sound that behave like the idealized dipole source described above, for example, pure‐tone fan noise, vibrating beams, unbaffled loudspeakers, and even wires and branches (which sing in the wind due to alternate side vortex shedding).
The next higher order source is the quadrupole. It is thought that the sound produced by the mixing process in an air jet gives rise to stresses that are quadrupole in nature. Quadrupoles may be considered to consist of two opposing point forces (two opposing dipoles) or equivalently four monopoles (see Table 3.1). We note that some authors use slightly different but equivalent definitions for the source strength of monopoles, dipoles, and quadrupoles. The definitions used in Sections 3.6and 3.7of this chapter are the same as in Crocker and Price [4] and Fahy [13] and result in expressions for sound pressure, sound intensity, and sound power which, although equivalent, are different in form from those in Ref. [20], for example.
The expression for the sound pressure for a quadrupole is even more complicated than for a dipole. Close to the source, in the near field, the sound pressure p ∝ 1 /r 3. Farther from the sound source, p ∝ 1 /r 2; while in the far field, p ∝ 1 /r .
Sound sources experienced in practice are normally even more complicated than dipoles or quadrupoles. The sound radiation from a vibrating piston is described in Refs. [6, 16, 17, 21]. Chapters 9and 11in the Handbook of Acoustics [1] also describe radiation from dipoles and quadrupoles and the sound radiation from vibrating cylinders in chapter 9 of the same book [1].
The discussion in Ref. [21] considers steady‐state radiation. However, there are many sources in nature and created by people that are transient. As shown in chapter 9 of the Handbook of Acoustics , [1] the harmonic analysis of these cases is often not suitable, and time‐domain methods have given better results and understanding of the phenomena. These are the approaches adopted in chapter 9 of the Handbook of Acoustics [1].
The radial particle velocity in a nondirectional spherically spreading sound field is given by Euler's equation as
(3.37) 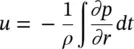
and substituting Eqs. (3.34)and (3.37)into (3.15)and then using Eq. (3.35)and time averaging gives the magnitude of the radial sound intensity in such a field as
(3.38) 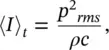
the same result as for a plane wave. The sound intensity decreases with the inverse square of the distance r . Simple omnidirectional monopole sources radiate equally well in all directions. More complicated idealized sources such as dipoles, quadrupoles, and vibrating piston sources create sound fields that are directional. Of course, real sources such as machines produce even more complicated sound fields than these idealized sources. (For a more complete discussion of the sound fields created by idealized sources, see Ref. [21] and chapters 3 and 8 in the Handbook of Acoustics [1].) However, the same result as Eq. (3.38)is found to be true for any source of sound as long as the measurements are made sufficiently far from the source. The intensity is not given by the simple result of Eq. (3.38)close to idealized sources such as dipoles, quadrupoles, or more complicated real sources of sound such as vibrating structures.
Close to such sources Eq. (3.15)must be used for the instantaneous radial intensity, and
(3.39) 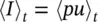
for the time‐averaged radial intensity.
The time‐averaged radial sound intensity in the far field of a dipole is given by [4]
(3.40) 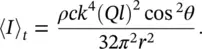
3.7 Sound Power of Sources
3.7.1 Sound Power of Idealized Sound Sources
The sound power W of a sound source is given by integrating the intensity over any imaginary closed surface S surrounding the source (see Figure 3.7):
(3.41) 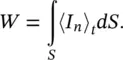
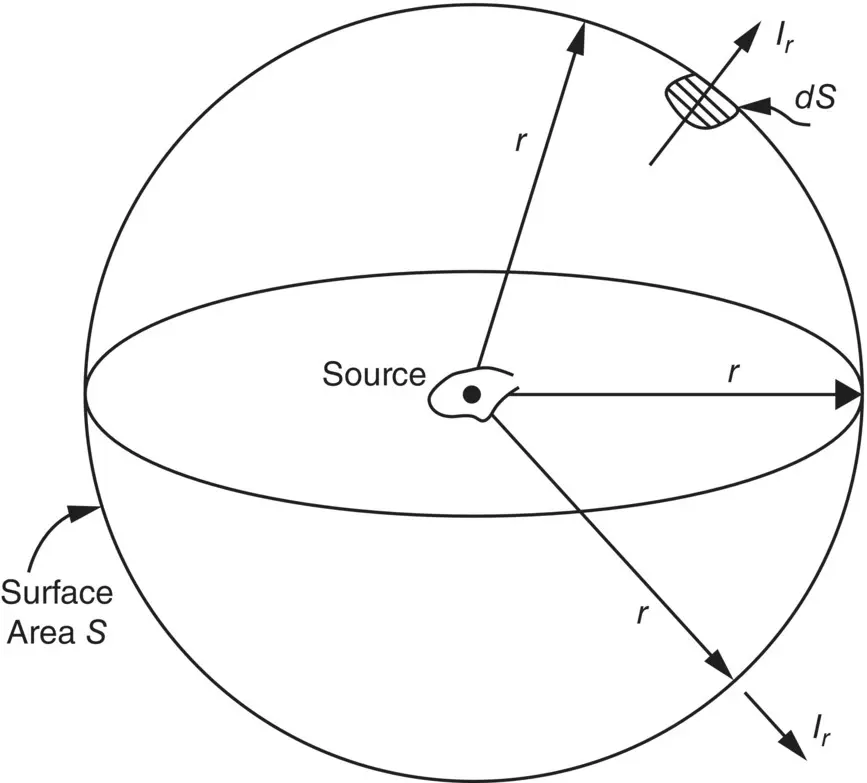
Figure 3.7 Imaginary surface area S for integration.
The normal component of the intensity I nmust be measured in a direction perpendicular to the elemental area dS . If a spherical surface, whose center coincides with the source, is chosen, then the sound power of an omnidirectional (monopole) source is
(3.42) 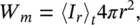
(3.43) 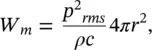
and from Eq. (3.35)the sound power of a monopole is [4, 13]
(3.44) 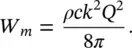
It is apparent from Eq. (3.44)that the sound power of an idealized (monopole) source is independent of the distance r from the origin, at which the power is calculated. This is the result required by conservation of energy and also to be expected for all sound sources.
Equation (3.43)shows that for an omnidirectional source (in the absence of reflections) the sound power can be determined from measurements of the mean square sound pressure made with a single microphone. Of course, for real sources, in environments where reflections occur, measurements should really be made very close to the source, where reflections are presumably less important.
The sound power of a dipole source is obtained by integrating the intensity given by Eq. (3.40)over a sphere around the source. The result for the sound power is
Читать дальше