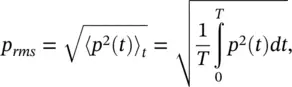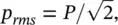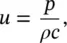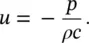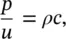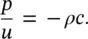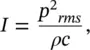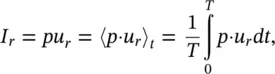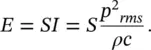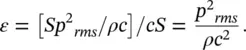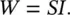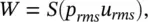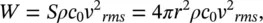Malcolm J. Crocker - Engineering Acoustics

where 〈〉 tdenotes a time average.

It is usually convenient to use the square root of the mean square pressure:

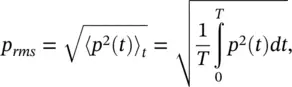
which is known as the root mean square (rms) sound pressure. This result is true for all cases of continuous sound time histories including noise and pure tones. For the special case of a pure tone sound, which is simple harmonic in time, given by p = P cos( ωt ), the rms sound pressure is

(3.9)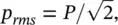

where P is the sound pressure amplitude.

As the piston vibrates, the gas immediately next to the piston must have the same velocity as the piston. A small element of fluid is known as a particle , and its velocity, which can be positive or negative, is known as the particle velocity . For waves traveling away from the piston in the positive x‐ direction, it can be shown that the particle velocity, u , is given by

(3.10)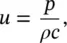

where ρ = fluid density (kg/m 3) and c = speed of sound (m/s).

If a wave is reflected by an obstacle, so that it is traveling in the negative x -direction, then

(3.11)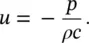

The negative sign results from the fact that the sound pressure is a scalar quantity, while the particle velocity is a vector quantity. These results are true for any type of plane sound waves, not only for sinusoidal waves.

We see that for the one‐dimensional propagation considered, the sound wave disturbances travel with a constant wave speed c , although there is no net, time‐averaged movement of the air particles. The air particles oscillate back and forth in the direction of wave propagation ( x‐ a x is) with velocity u . We may show that for any plane wave traveling in the positive x direction at any instant

(3.12)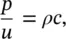

and for any plane wave traveling in the negative x‐ direction

(3.13)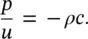

The quantity ρ c is known as the characteristic impedance of the fluid, and for air, ρ c = 428 kg s/m 2at 0 °C and 415 kg s/m 2at 20 °C.

The intensity of sound, I , is the time‐averaged sound energy that passes through unit cross‐sectional area in unit time. For a plane progressive wave, or far from any source of sound (in the absence of reflections):

(3.14)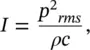

where ρ = the fluid density (kg/m 3) and c = speed of sound (m/s).

In the general case of sound propagation in a three‐dimensional field, the sound intensity is the (net) flow of sound energy in unit time flowing through unit cross‐sectional area. The intensity has magnitude and direction

(3.15)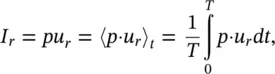

where p is the total fluctuating sound pressure and u ris the total fluctuating sound particle velocity in the r‐ direction at the measurement point. The total sound pressure p and particle velocity u rinclude the effects of incident and reflected sound waves.

We note, in general, for sound propagation in three dimensions that the instantaneous sound intensity Iis a vector quantity equal to the product of the scalar sound pressure and the instantaneous vector particle velocity u . Thus Ihas magnitude and direction. The vector intensity Imay be resolved into components I x, I y, and I z. For a more complete discussion of sound intensity and its measurement see Chapter 8in this book, chapters 45 and 156 in the Handbook of Acoustics [1] and the book by Fahy [13].

Consider the case again of the oscillating piston in Figure 3.1. We shall consider the sound energy that is produced by the oscillating piston, as it flows along the tube from the piston source. We observe that the wavefront and the sound energy travel along the tube with velocity c metres/second. Thus after one second, a column of fluid of length c m contains all of the sound energy provided by the piston during the previous second. The total amount of energy E in this column equals the time‐averaged sound intensity multiplied by the cross‐sectional area S , which is from Eq. (3.9):

(3.16)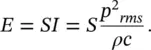

The sound energy per unit volume is known as the energy density ε ,

(3.17)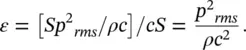

This result in Eq. (3.17)can also be shown to be true for other acoustic fields as well, as long as the total sound pressure is used in Eq. (3.17), and provided the location is not very close to a sound source.

Again in the case of the oscillating piston, we will consider the sound power radiated by the piston into the tube. The sound power radiated by the piston, W , is

(3.18)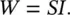

But from Eqs. (3.10)and (3.14)the power is

(3.19)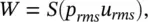

and close to the piston, the rms particle velocity, u rms, must be equal to the rms piston velocity. From Eq. (3.19), we can write

(3.20)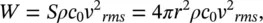

where r is the piston and duct radius, and v rmsis the rms velocity of the piston.

The range of sound pressure magnitudes and sound powers of sources experienced in practice is very large. Thus, logarithmic rather than linear measures are often used for sound pressure and sound power. The most common measure of sound is the decibel . Decibels are also used to measure vibration, which can have a similar large range of magnitudes. The decibel represents a relative measurement or ratio. Each quantity in decibels is expressed as a ratio relative to a reference sound pressure , sound power , or sound intensity , or in the case of vibration relative to a reference displacement , velocity , or acceleration . Whenever a quantity is expressed in decibels, the result is known as a level .