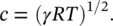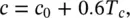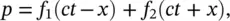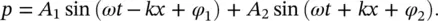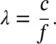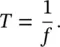Malcolm J. Crocker - Engineering Acoustics

where p is the sound pressure, x is the coordinate, and t is the time.

This equation is known as the one‐dimensional equation of motion, or acoustic wave equation. Similar wave equations may be written if the sound pressure p in Eq. (3.1)is repla c ed with the particle displacement ξ , the particle velocity u , condensation s , fluctuating density ρ′ , or the fluctuating absolute temperature T′ . The derivation of these equations is in general more complicated. However, the wave equation in terms of the sound pressure in Eq. (3.1)is perhaps most useful since the sound pressure is the easiest acoustical quantity to measure (using a microphone) and is the acoustical perturbation we sense with our ears. It is normal to write the wave equation in terms of sound pressure p , and to derive the other variables, ξ , u , s , ρ ′ , and T′ from their relations with the sound pressure p [16]. The sound pressure p is the acoustic pressure perturbation or fluctuation about the time‐averaged, or undisturbed, pressure p 0.

The speed of sound waves c is given for a perfect gas by

(3.2)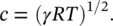

The speed of sound is proportional to the square root of the absolute temperature T . The ratio of specific heats γ and the gas constant R are constants for any particular gas. Thus Eq. (3.2)may be written as

(3.3)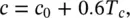

where, for air, c 0= 331.6 m/s, the speed of sound at 0 °C, and T cis the temperature in degrees Celsius. Note that Eq. (3.3)is an appro x imate formula valid for T cnear room temperature. The speed of sound in air is almost completely dependent on the air temperature and is almost independent of the atmospheric pressure. For a complete discussion of the speed of sound in fluids, see chapter 5 in the Handbook of Acoustics [1].

A solution to Eq. (3.1)is

(3.4)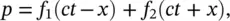

where f 1and f 2are arbitrary functions such as sine, cosine, e x ponential, log, and so on. It is easy to show that Eq. (3.4)is a solution to the wave equation Eq. (3.1)by differentiation and substitution into Eq. (3.1). Varying x and t in Eq. (3.4)demonstrates that f 1( ct − x ) represents a wave traveling in the positive x‐ direction with wave speed c , while f 2( ct + x ) represents a wave traveling in the negative x‐ direction with wave speed c (see Figure 3.2).

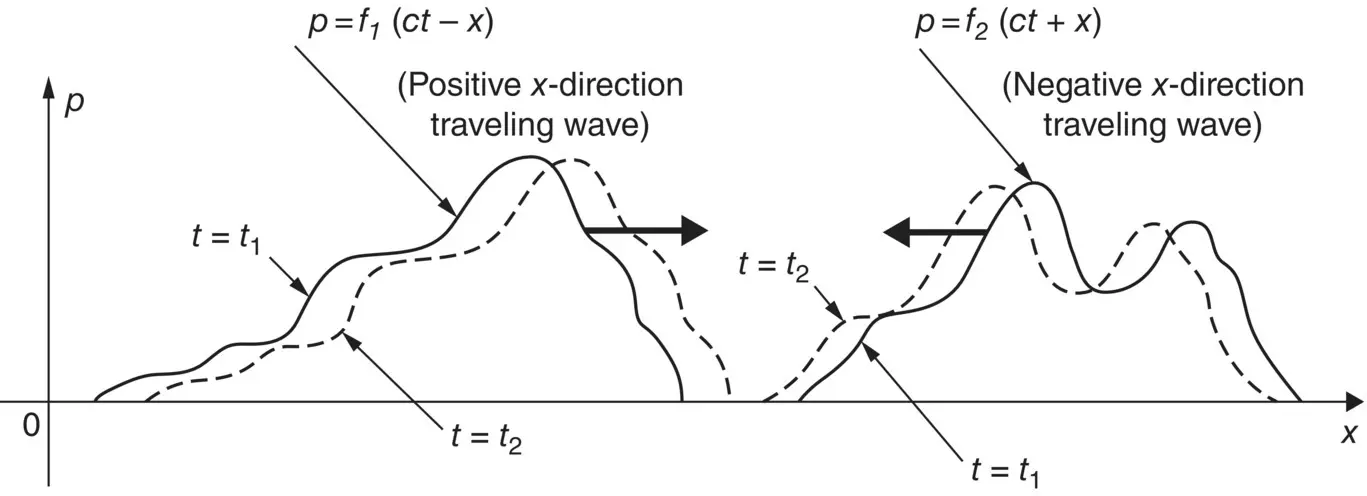
Figure 3.2 Plane waves of arbitrary waveform.

The solution given in Eq. (3.4)is usually known as the general solution since, in principle, any type of sound waveform is possible. In practice, sound waves are usually classified as impulsive or steady in time. One particular case of a steady wave is of considerable importance. Waves created by sources vibrating sinusoidally in time (e.g.a loudspeaker, a piston, or a more complicated structure vibrating with a discrete angular frequency ω ) both in time t and space x in a sinusoidal manner (see Figure 3.3):

(3.5)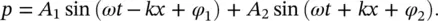

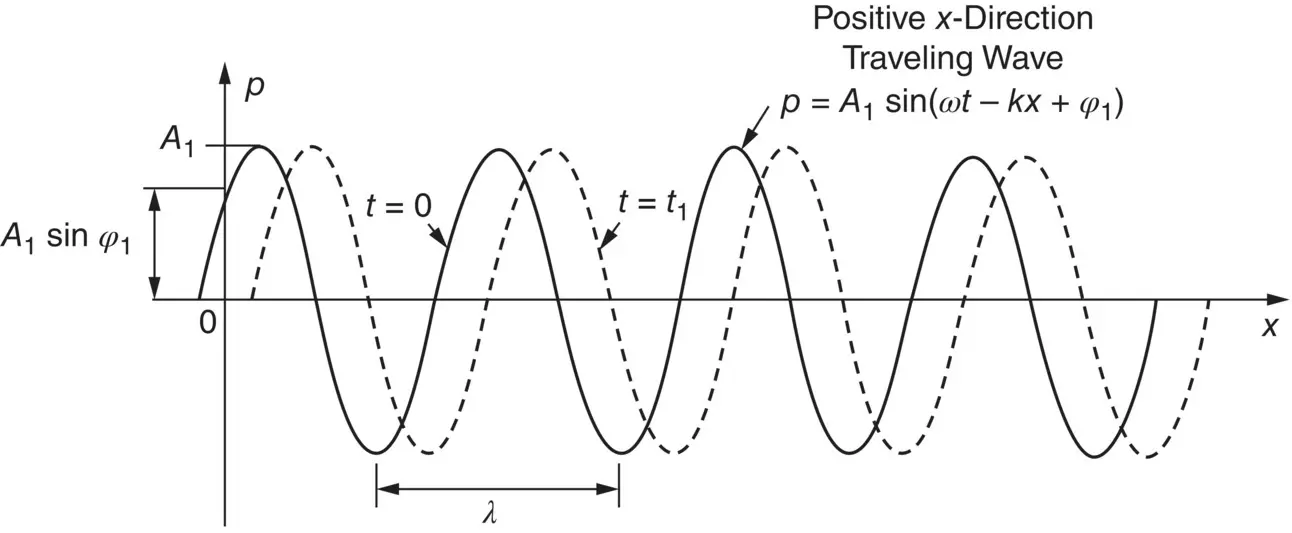
Figure 3.3 Simple harmonic plane waves.

At any point in space, x , the sound pressure p is simple harmonic in time. The first expression on the right of Eq. (3.5)represents a wave of amplitude A 1traveling in the positive x‐ direction with speed c , while the second expression represents a wave of amplitude A 2traveling in the negative x‐ direction. The symbols ϕ 1and ϕ 2are phase angles, and k is the acoustic wavenumber . It is observed that the wavenumber k = ω/c by studying the ratio of x and t in Eqs. (3.4)and (3.5). At some instant t the sound pressure pattern is sinusoidal in space, and it repeats itself each time kx is increased by 2 π . Such a repetition is called a wavelength λ . Hence, kλ = 2 π or k = 2 π/λ . This gives ω/c = 2 π/c = 2 π/λ , or

(3.6)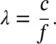

The wavelength of sound becomes smaller as the frequency is increased. In air, at 100 Hz, λ ≈ 3.5 m ≈ 10 ft. At 1000 Hz, λ ≈ 0.35 m ≈ 1 ft. At 10000 Hz, λ ≈ 0.035 m ≈ 0.1 ft. ≈ 1 in.

At some point x in space, the sound pressure is sinusoidal in time and goes through one complete cycle when ω increases by 2 π . The time for a cycle is called the period T . Thus, ωT = 2 π , T = 2 π/ω , and

(3.7)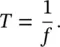

The human audible frequency range is from 20 Hz to 20 kHz. Calculate the extremes of wavelength for audible sounds at 20 °C.

From Eq. (3.3)the speed of sound at 20 °C is c = 331.6 + 0.6(20) = 343.6 m/s. Therefore, using Eq. (3.6)the wavelength of a sound of 20 Hz is λ = 343.6/20 = 17.18 m. The wavelength of a sound of 20 kHz is λ = 343.6/20000 = 0.01718 m = 17.18 mm.

With sound waves in a fluid such as air, the sound pressure at any point is the difference between the total pressure and normal atmospheric pressure. The sound pressure fluctuates with time and can be positive or negative with respect to the normal atmospheric pressure.

Sound varies in magnitude and frequency and it is normally convenient to give a single number measure of the sound by determining its time‐averaged value. The time average of the sound pressure at any point in space, over a sufficiently long time, is zero and is of no interest or use. The time average of the square of the sound pressure, known as the mean square pressure, however, is not zero. If the sound pressure at any instant t is p ( t ), then the mean square pressure, 〈 p 2( t )〉 t, is the time average of the square of the sound pressure over the time interval T :

(3.8)