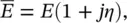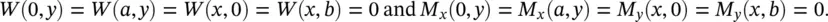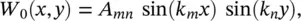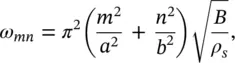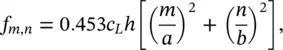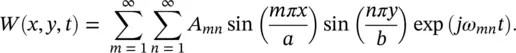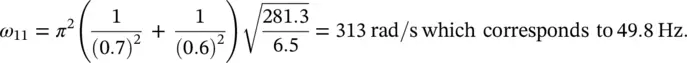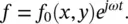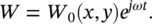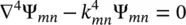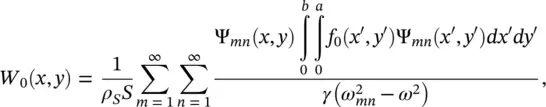Malcolm J. Crocker - Engineering Acoustics

(2.67)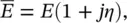

where η is the internal loss factor of the plate. As an example, Figure 2.17shows the computation of the velocity level response in decibels of the first resonance in a clamped‐clamped rectangular panel and the effect of varying its internal loss factor η .

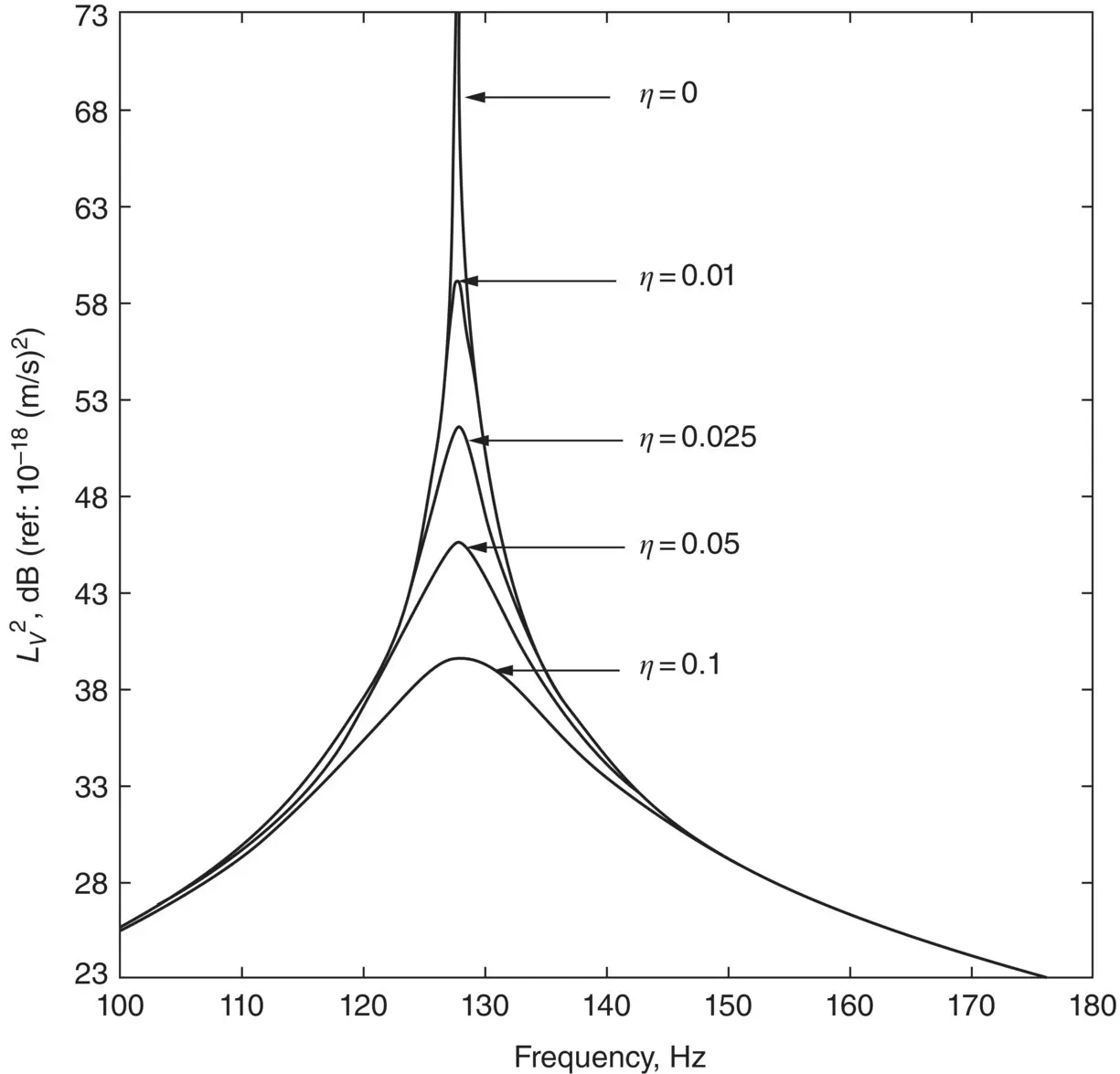
Figure 2.17 Velocity level of a fully‐clamped rectangular plate as a function of frequency for selected values of η . The resonance of its first mode is shown. The plate is a plywood board with properties E = 6 × 10 9N/m 2, ρ s= 6.5 kg/m 2, S = a × b = 0.7 × 0.6 m 2, and ν = 0.3. (

Source: from Ref. [16].)

The free vibration of plates has two important characteristics:

1 The velocity of propagation of flexural waves in the plate depends on frequency, and

2 The second component of the deflection, arising as a result of the stiffness of the plate, brings about additional changes, compared to a beam, in the distribution of the vibration.

As in the case of beams, plates can be fixed at their edges in various manners. Solutions for vibrating plates subjected to different boundary conditions have been discussed in several books for the 27 possible combinations [14, 17]. In this section we will discuss a uniform simply supported plate of length a and width b , mainly because this problem is illustrative and it has a closed‐form solution. In this case, the plate at its supports cannot perform motion perpendicular to its surface, but can rotate around the edge, and hence the displacement and bending moment are zero at the corresponding boundaries (see Eq. (2.55)for a beam)

(2.68)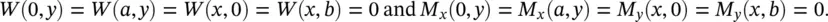

The solution for the amplitude of flexural vibrations of a simply‐supported plate vibrating in mode ( m,n ), where m −1 and n −1 are the number of nodal lines in the x and y directions, respectively, can be obtained by separation of variables and is given by [14]

(2.69)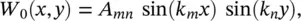

where A mnis the modal amplitude, k m= mπ / a , k n= nπ / b and m and n are integers. Equation (2.69)gives the mode shapes of the simply‐supported plate. Figure 2.18shows the first six mode shapes of a rectangular plate. Natural frequencies of each plate's mode ( m,n ) are given by

(2.70a)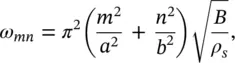

where ρ sis the mass of the plate per unit surface area. Note that Eq. (2.70a)can be approximated by

(2.70b)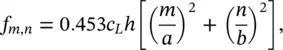

where f m,nis the characteristic modal frequency (Hz) and c Lis the longitudinal wave speed in the plate material (m/s).

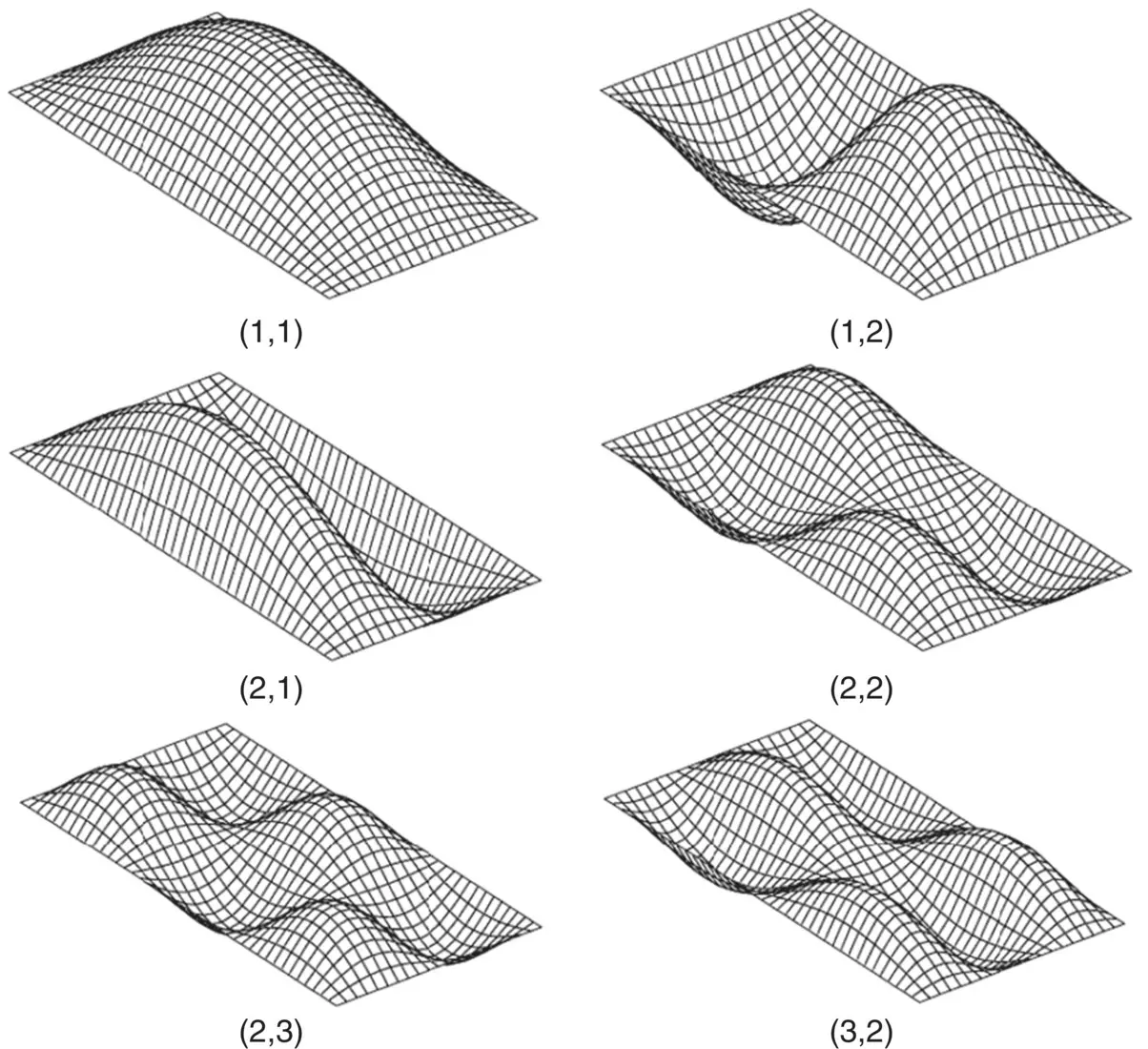
Figure 2.18 First six modes of a rectangular plate.

Thus, the total solution for the free vibration of a simply‐supported plate is

(2.71)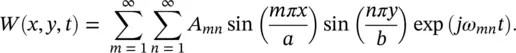

Note that for a square plate ( a = b ) ω mn = ω nm. Therefore modes ( m,n ) and ( n,m ) have the same frequency and they are called degenerate . This fact also happens when the length or width are integer multiple of each other.

Determine the natural frequency of the fundamental mode of a plywood board of thickness 8 mm, mass density 812.5 kg/m 3, and dimensions a × b = 0.7 × 0.6 m 2.

The plywood board has properties E = 6 × 10 9N/m 2, S = a × b = 0.7 × 0.6 m 2, and ν = 0.3. The mass of the plate per unit surface area ρ s= ρ × h = 812.5 × 0.008 = 6.5 kg/m 2. and the bending stiffness B = Eh 3/12(1 − ν 2) = 6 × 10 9(0.008) 3/12 (1 − [0.3] 2) = 281.3 N/m. Then, the fundamental mode (the lowest natural frequency) is given for m = n = 1. Replacing the values in Eq. (2.70a)yields

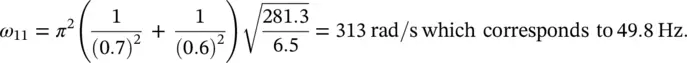
b) Forced Vibration of a Rectangular Plate

Let us assume that a distributed harmonic force acts on a rectangular plate (referred to unit plate area)

(2.72)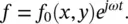

Under the influence of this force, a plate deflection W is produced with the distribution

(2.73)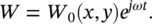

The distribution of the deflection amplitude W 0can be represented by the resultant of a series of sinusoidal vibrations. The frequency is equal to the frequency of free vibration of the plate, that is to say, the following equation must be satisfied [18]

(2.74)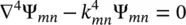

where k mn= ω mn/ c bis the wavenumber of the ( m,n ) mode of free vibration, c bis the velocity of bending waves in the plate and Ψ mnare the dimensionless coefficients which determine the relative distribution in relation to the maximum amplitude of deflection.

Using the orthogonality of the function Ψ mnand Fourier series, the resultant distribution of vibration on the rectangular plate is given by [16]

(2.75)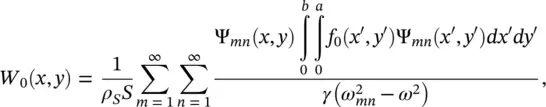

where ( x ′, y ′) denotes the coordinates of the position of the force f (referred to unit plate area), with respect to which the integration is carried out over the surface area of the plate. The ω mnare real numbers for a plate without losses. For the frequency of forced vibration ω = ω mn, the amplitude of the deflection grows theoretically to infinity. In a plate with losses, ω mnare complex numbers, as discussed in Section 2.4.3.