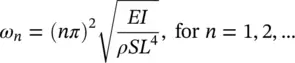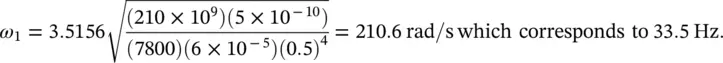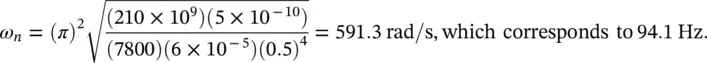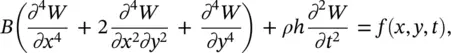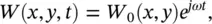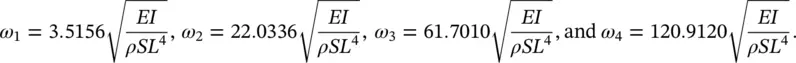
The mode shapes are given by [10, 13]
(2.62) 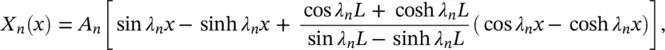
where A nis an arbitrary constant. Thus, the total solution for the free transverse vibration of the cantilever beam is
(2.63) 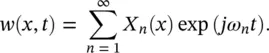
Figure 2.16shows the first four mode shapes for a cantilever beam.
Determine the natural frequencies of a uniform beam which is simply supported at both ends.
Applying the boundary conditions w = 0 and 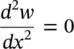 at x = 0 in Eq. (2.54)leads to C 1+ C 3= 0 and − λ 2 C 1+ λ 2 C 3= 0. These equations are satisfied if C 1= C 3= 0.
at x = 0 in Eq. (2.54)leads to C 1+ C 3= 0 and − λ 2 C 1+ λ 2 C 3= 0. These equations are satisfied if C 1= C 3= 0.
Applying the boundary conditions w = 0 and 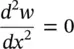 at x = L in Eq. (2.54)yields
at x = L in Eq. (2.54)yields
C 2sin( λL ) + C 4sinh( λL ) = 0 and − λ 2 C 2sin( λL ) + λ 2 C 4sinh( λL ) = 0. Therefore, nontrivial solutions are obtained when C 4= 0 and sin( λL ) = 0, so λ = nπ / L (for n = 1,2,…). Since λ = ( ω 2 ρS / EI ) 1/4, we find that the natural frequencies ω nare given by
(2.64) 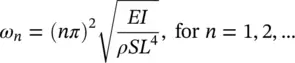
Determine the lowest natural frequency for a cantilever steel beam of thickness a = 6 mm, width b = 10 mm, and length L = 0.5 m. Repeat the calculation when the beam is simply supported at both ends.
For steel we have E = 210 × 10 9N/m 2and ρ = 7800 kg/m 3. The cross‐sectional moment of inertia of a rectangular beam is I = ab 3/12 = 0.006 × (0.01) 3/12 = 5 × 10 −10m 4. The cross‐sectional area of the beam is S = 0.006 × 0.01 = 6 × 10 −5m 2. Then,
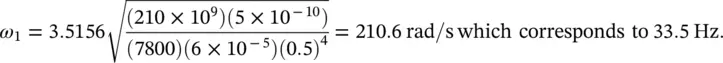
If the beam is now simply supported, we use Eq. (2.64)with n = 1,
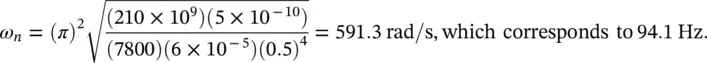
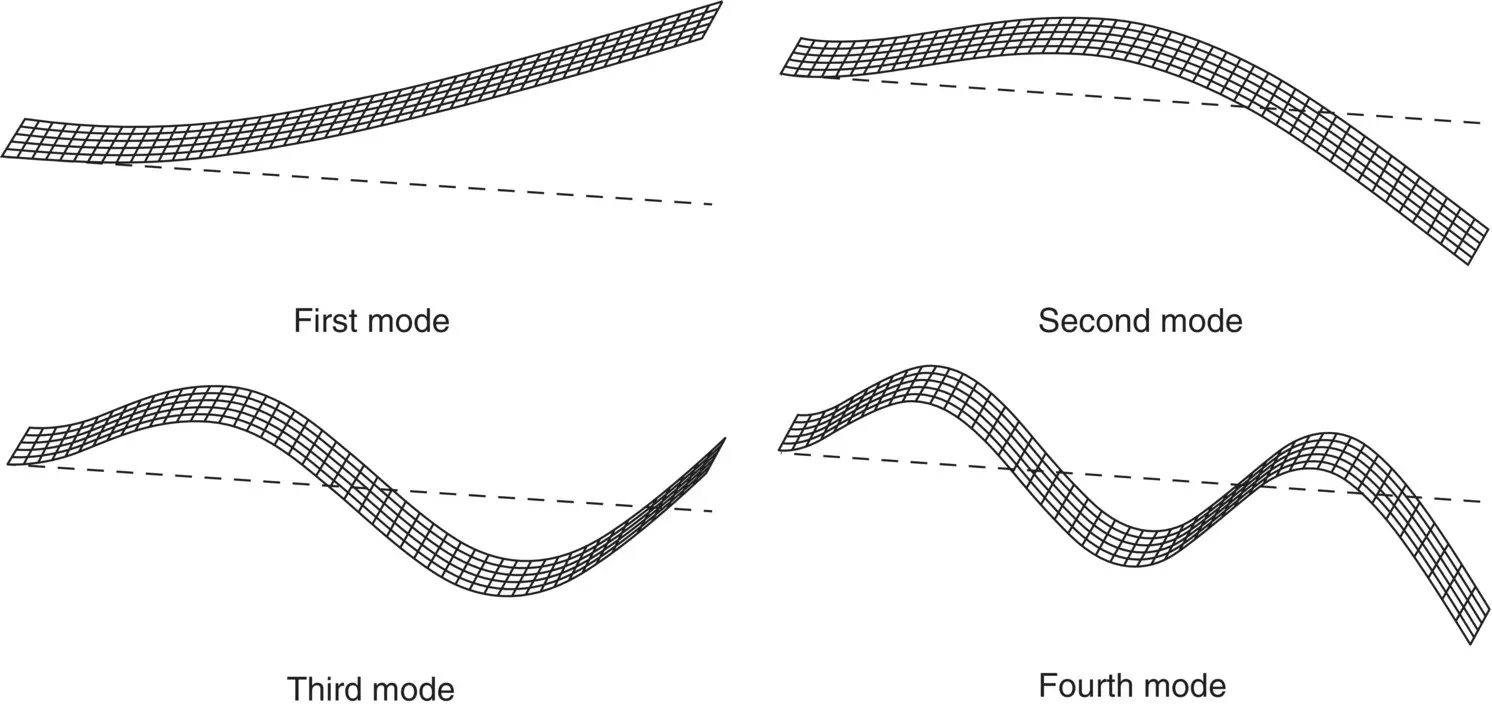
Figure 2.16 First four mode shapes of a cantilever beam.
2.5.2 Vibration of Thin Plates
The present section is concerned with systems possessing two dimensions which are large compared with the third, e.g. plates whose lengths and widths are much greater than their thicknesses. There are numerous applications of vibrating plates in electroacoustical equipment such as loudspeakers, microphones, earphones, ultrasonic transducers, etc. In addition, plates can be found as constituting elements in several mechanical systems such as cars, trains, aircraft, and machinery. Plates, considered as plane systems, are a particular case of shells, whose surface may be of any shape. The general theory of vibrations of shells, which constitutes a large branch of mechanics, has been discussed by Leissa [14]. In 1828, Poisson and Cauchy established, for the first time, an approximate differential equation for flexural vibrations of a plate of infinite extent, and Poisson obtained an approximate solution for a particular case of the vibration of a circular plate. The development by Ritz in 1909 of the method for calculating the bending of plates on the basis of the energy balance was an important advance. This method made it possible to solve more complicated cases of the vibration of plates having different shapes [11]. Further advances were accomplished by the accurate calculation of the vibration distribution in rectangular plates with uniform and mixed boundary conditions [15].
a) Free Vibrations of a Rectangular Plate
For the requirements of acoustical engineering, it is sufficient to consider the flexural vibrations of thin plates ( λ >> h , where h is the thickness of the plate) to which we can apply an approximate method analogous to that employed for bar [11].
The assumptions are:
1 The transverse cross‐sections of the plate still remain plane in the presence of strains, and
2 Neither longitudinal nor transverse strains occur on the middle (neutral) plane.
These conditions are satisfied approximately when the flexural wavelength is at least equal to a six times the thickness h of the plate. Under this assumption, the wave equation for transverse vibration of the plate is [14]
(2.65) 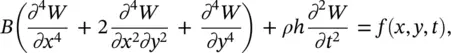
where W ( x,y,t ) is the instantaneous transverse displacement, ρ is the density of the plate, B = Eh 3/12(1 − ν 2) is the stiffness of the plate for bending, ν is the Poisson's ratio, E is the modulus of elasticity (Young's modulus) and f ( x,y,t ) are the external forces referring to unit surface area of the plate. The sum of the first three terms of Eq. (2.65)is a double Laplacian of W , ∇ 4 W , expressed in rectangular coordinates. It is useful to define the solution for steady‐state conditions as
(2.66) 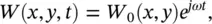
where W 0( x,y ) is the amplitude of the transverse displacement.
A vibrating structure, such as a plate, at any instant contains some kinetic energy and some strain (or potential) energy. The kinetic energy is associated with the mass and the strain energy is associated with the stiffness. In addition, any structure also dissipates some energy as it deforms. This conversion of ordered mechanical energy into thermal energy is called damping. A simple way to describe the energy loss is given by the analysis of the one‐dimensional system of Eq. (2.17). Thus, for sinusoidal vibration, use of a spring with an appropriately defined stiffness is completely equivalent to the use of an elastic spring and a dashpot. The internal losses in a plate arise not because of the motion of the plate as a whole body, but depend on the mutual displacements of the neighboring elements of the plate, and these are proportional to the changes in time of ∇ 4 W . Therefore, in order to account for energy dissipation in a plate, one may simply introduce a complex modulus of elasticity
Читать дальше

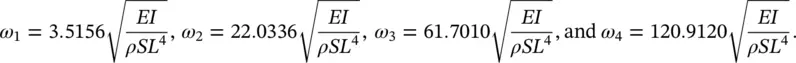
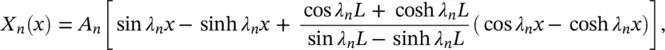
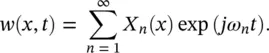
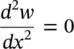 at x = 0 in Eq. (2.54)leads to C 1+ C 3= 0 and − λ 2 C 1+ λ 2 C 3= 0. These equations are satisfied if C 1= C 3= 0.
at x = 0 in Eq. (2.54)leads to C 1+ C 3= 0 and − λ 2 C 1+ λ 2 C 3= 0. These equations are satisfied if C 1= C 3= 0.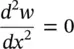 at x = L in Eq. (2.54)yields
at x = L in Eq. (2.54)yields