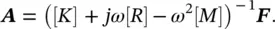(2.39) 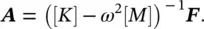
If we consider the two‐degree of freedom system discussed in Example 2.5but now harmonic force excitations of frequency ω and amplitude F 1and F 2are applied to the masses m 1and m 2, respectively (see Figure 2.13), the equations of motion are
(2.40a) 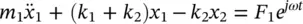
and
(2.40b) 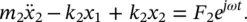
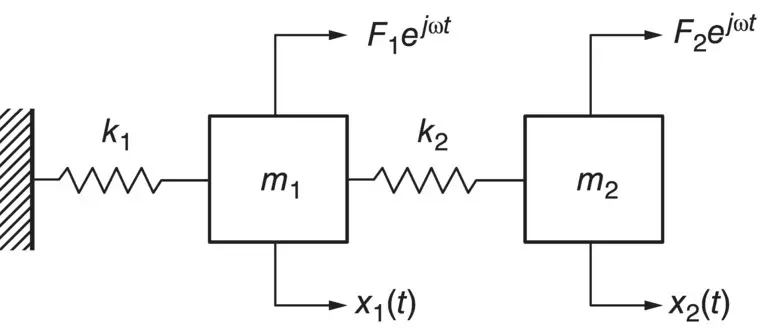
Figure 2.13 Harmonically forced two‐degree‐of‐freedom system.
The particular solution is given by Eq. (2.36)as
(2.41) 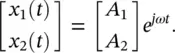
Therefore, Eq. (2.37)becomes
(2.42) 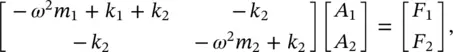
which has to be simultaneously solved to find the displacement amplitudes A 1and A 2.
Let consider the two‐degree of freedom system of Example 2.5. Assume that a force F 0 e jωtis applied to mass m 1and no force is applied to mass m 2. Then, Eq. (2.37)becomes
(2.43) 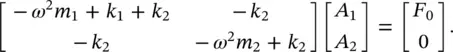
Solving the system of Eq. (2.43)simultaneously, we obtain that
(2.44) 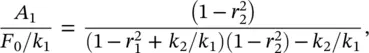
(2.45) 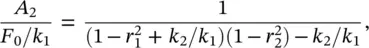
and the ratio
(2.46) 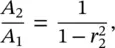
where 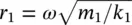 and
and 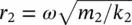 .
.
It is noted from Eq. (2.44)that the steady‐state amplitude of the mass m 1will become zero when r 2= 1, i.e. when the excitation frequency is 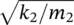 . Thus when the stiffness and mass of the secondary mass‐spring system are chosen correctly, the main mass theoretically does not move. At this frequency the secondary mass is exactly 180° out‐of‐phase with the force applied to the primary mass and the mass has an amplitude A 2= − F 0/ k 2. This is the concept of the dynamic vibration absorber (also called neutralizer) used in machinery vibration control applications [11, 13]. The applied force is canceled by an equal and opposite force from the secondary spring. The dynamic vibration absorber was invented in 1909 by Hermann Frahm. This technique works when the excitation is at a fixed frequency at or close to resonance. Since the total system has two natural frequencies (one either side of the excitation frequency), a change in the frequency of the excitation force could excite the modified system at one of these frequencies, making the vibration absorber ineffective.
. Thus when the stiffness and mass of the secondary mass‐spring system are chosen correctly, the main mass theoretically does not move. At this frequency the secondary mass is exactly 180° out‐of‐phase with the force applied to the primary mass and the mass has an amplitude A 2= − F 0/ k 2. This is the concept of the dynamic vibration absorber (also called neutralizer) used in machinery vibration control applications [11, 13]. The applied force is canceled by an equal and opposite force from the secondary spring. The dynamic vibration absorber was invented in 1909 by Hermann Frahm. This technique works when the excitation is at a fixed frequency at or close to resonance. Since the total system has two natural frequencies (one either side of the excitation frequency), a change in the frequency of the excitation force could excite the modified system at one of these frequencies, making the vibration absorber ineffective.
Repeat the problem discussed in Example 2.6but now assume that a force F 0 e jωtis applied to the mass m 2and no force is applied to the mass m 1.
Equation (2.37)becomes now
(2.47) 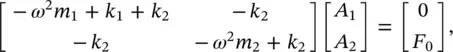
which leads to the following results
(2.48) 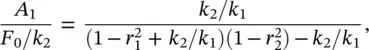
(2.49) 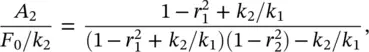
where 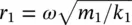 and
and 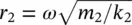 .
.
If there is damping present (as there always is in real systems) the homogenous solution of a harmonically forced vibration system decays away with time. It has to be noted that when damping is included in the mathematical model, the eigenvalues and eigenvectors can be complex numbers, unlike in the undamped case. Although in practice the damping of a structural system is often small, its effect on the system response at or near resonance may be significant. If the damping matrix is a linear combination of the mass and the stiffness matrix ( proportional damping ), the system of differential Eq. (2.22)can be uncoupled using the modal matrix method [13]. This method is based on calculating the eigenvalues and eigenvectors of the system and the application of a modal transformation in a new set of coordinates called modal coordinates . This technique is not possible to apply if the damping matrix is arbitrary. In this case, a state‐space representation is often used to uncouple the system [10]. This technique reduces the order of the differential equations at the expense of doubling the number of degrees of freedom.
For the case of an n ‐degree of freedom system with viscous damping and subject to a single‐frequency harmonic excitation, we can assume harmonic solutions in the form of Eq. (2.36)and use the same arguments employed to obtain Eq. (2.39). Thus, the amplitudes of Eq. (2.36)are now expressed as [13]
(2.50) 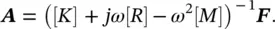
Several examples are discussed in textbooks on vibration theory [10–13].
Equation (2.50)shows that if the forcing frequency is very low in comparison to the lowest natural frequency, the term [ K ] is dominant and the vibration amplitudes are controlled mainly by the system's stiffness. If the system is excited significantly above their resonance frequency region, the term − ω 2[ M ] dominates and the system is mass‐controlled. Damping only has an appreciable effect around the resonance frequencies. The effects of these frequency regions on the sound transmitted through a forced vibrating panel are discussed in Chapter 12.
Читать дальше

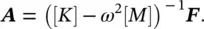
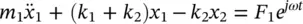
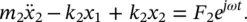

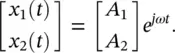
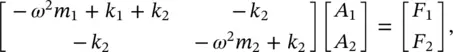
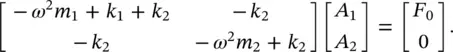
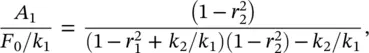
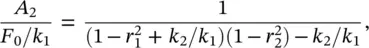
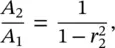
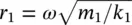 and
and 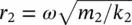 .
.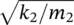 . Thus when the stiffness and mass of the secondary mass‐spring system are chosen correctly, the main mass theoretically does not move. At this frequency the secondary mass is exactly 180° out‐of‐phase with the force applied to the primary mass and the mass has an amplitude A 2= − F 0/ k 2. This is the concept of the dynamic vibration absorber (also called neutralizer) used in machinery vibration control applications [11, 13]. The applied force is canceled by an equal and opposite force from the secondary spring. The dynamic vibration absorber was invented in 1909 by Hermann Frahm. This technique works when the excitation is at a fixed frequency at or close to resonance. Since the total system has two natural frequencies (one either side of the excitation frequency), a change in the frequency of the excitation force could excite the modified system at one of these frequencies, making the vibration absorber ineffective.
. Thus when the stiffness and mass of the secondary mass‐spring system are chosen correctly, the main mass theoretically does not move. At this frequency the secondary mass is exactly 180° out‐of‐phase with the force applied to the primary mass and the mass has an amplitude A 2= − F 0/ k 2. This is the concept of the dynamic vibration absorber (also called neutralizer) used in machinery vibration control applications [11, 13]. The applied force is canceled by an equal and opposite force from the secondary spring. The dynamic vibration absorber was invented in 1909 by Hermann Frahm. This technique works when the excitation is at a fixed frequency at or close to resonance. Since the total system has two natural frequencies (one either side of the excitation frequency), a change in the frequency of the excitation force could excite the modified system at one of these frequencies, making the vibration absorber ineffective.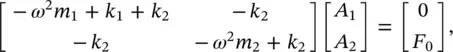
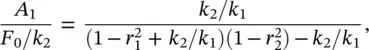
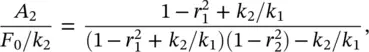
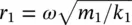 and
and 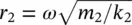 .
.