A 600‐kg machine is mounted on springs such that its static deflection is 2 mm. Determine the damping constant of a viscous damper to be added to the system in parallel with the springs, such that the system is critically damped.
The static deflection is given by Eq. (2.8a)as d = Mg / K . Therefore K = Mg / d = 600(9.8)/2 × 10 −3= 294 × 10 4N/m. The system is critically damped when the damped constant R crit= (4 MK ) 1/2= (4 × 600 × 294 × 10 4) 1/2= 84 000 Ns/m.
(c) Forced Vibration – Damped
If a damped spring–mass system is excited by a simple harmonic force at some arbitrary angular forcing frequency ω (see Figure 2.8), we now obtain the equation of motion Eq. (2.17):
(2.17) 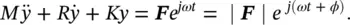
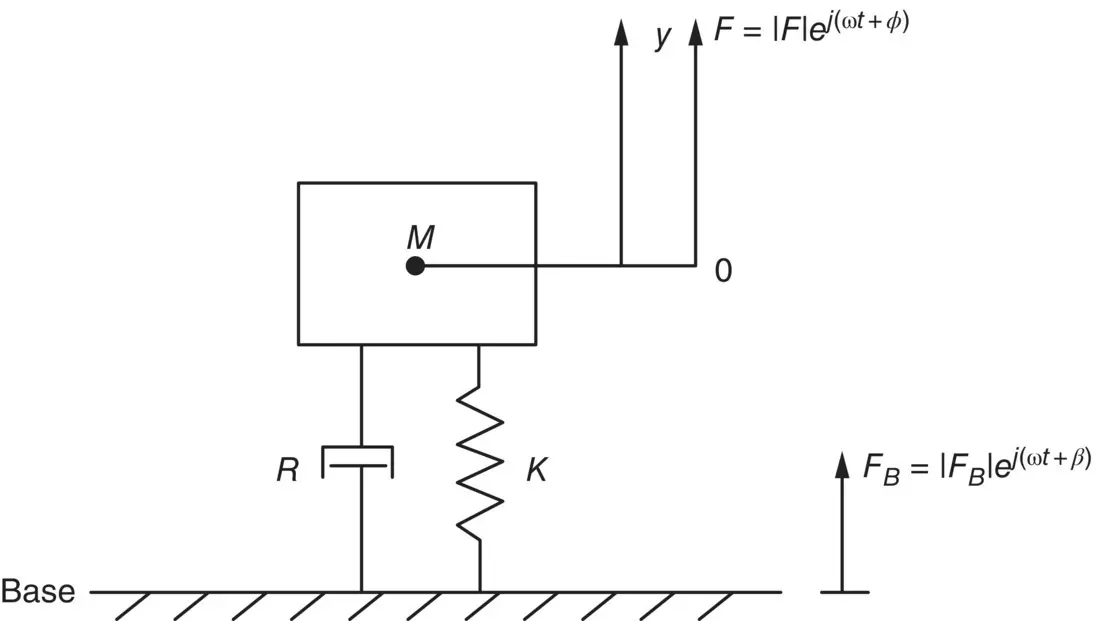
Figure 2.8 Forced vibration of damped simple system.
The force Fis normally written in the complex form for mathematical convenience. The real force acting is, of course, the real part of For | F| cos( ωt ), where | F| is the force amplitude.
If we assume a solution of the form y = A e jωtthen we obtain from Eq. (2.17):
(2.18) 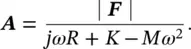
We can write A= | A| e jα, where α is the phase angle between force and displacement. The phase, α , is not normally of much interest, but the amplitude of motion | A| of the mass is. The amplitude of the displacement is
(2.19) 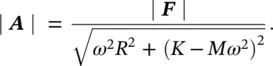
This can be expressed in alternative form:
(2.20) 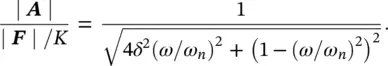
Equation (2.20)is plotted in Figure 2.9. It is observed that if the forcing frequency ω is equal to the natural frequency of the structure, ω n, or equivalently f = f n, a condition called resonance, then the amplitude of the motion is proportional to 1/(2 δ ). The ratio | A| / (| F| /K ) is sometimes called the dynamic magnification factor (DMF). The number | F| /K is the static deflection the mass would assume if exposed to a constant nonfluctuating force | F|. If the damping ratio, δ , is small, the displacement amplitude A of a structure excited at its natural or resonance frequency is very high. For example, if a simple system has a damping ratio, δ , of 0.01, then its dynamic displacement amplitude is 50 times (when exposed to an oscillating force of | F| N) its static deflection (when exposed to a static force of amplitude | F| N), that is, DMF = 50.

Figure 2.9 Dynamic magnification factor (DMF) for a damped simple system.
Situations such as this should be avoided in practice, wherever possible. For instance, if an oscillating force is present in some machine or structure, the frequency of the force should be moved away from the natural frequencies of the machine or structure, if possible, so that resonance is avoided. If the forcing frequency f is close to or coincides with a natural frequency f n, large amplitude vibrations can occur with consequent vibration and noise problems and the potential of serious damage and machine malfunction.
The force on the idealized damped simple system will create a force on the base 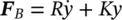 . Substituting this into Eq. (2.17)and rearranging and finally comparing the amplitudes of the imposed force | F| with the force transmitted to the base | F B| gives
. Substituting this into Eq. (2.17)and rearranging and finally comparing the amplitudes of the imposed force | F| with the force transmitted to the base | F B| gives
(2.21) 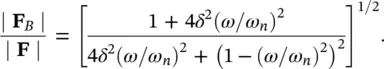
Equation (2.21)is plotted in Figure 2.10. The ratio | F B| / | F| is sometimes called the force transmissibility T F. The force amplitude transmitted to the machine support base, F B, is seen to be much greater than 1, if the exciting frequency is at the system resonance frequency. The results in Eq. (2.21)and Figure 2.10have important applications to machinery noise problems that will be discussed again in detail in Chapter 9of this book.
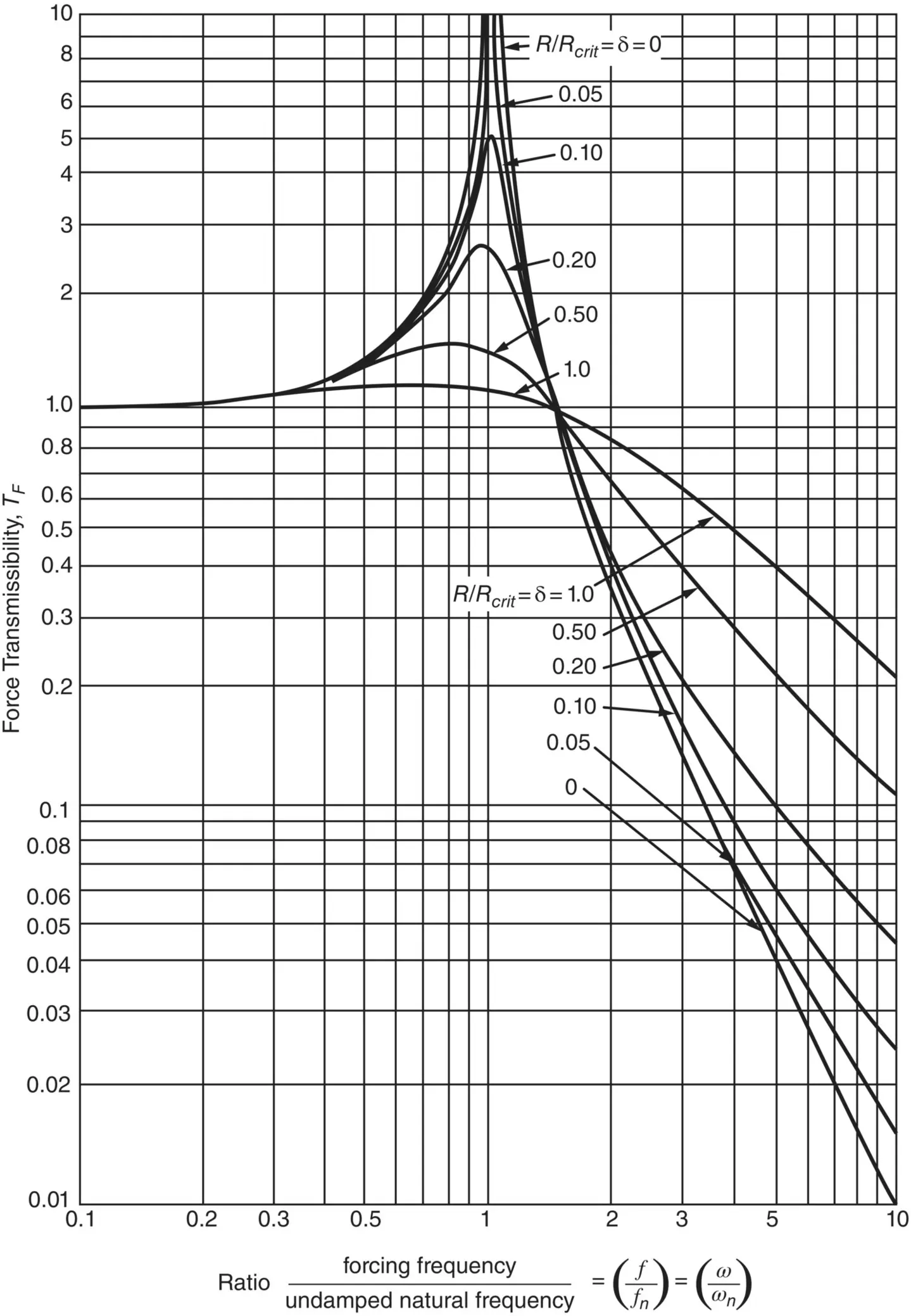
Figure 2.10 Force transmissibility, T F, for a damped simple system.
Briefly, we can observe that these results can be utilized in designing vibration isolators for a machine. The natural frequency ω nof a machine of mass M resting on its isolators of stiffness K and damping constant R must be made much less than the forcing frequency ω . Otherwise, large force amplitudes will be transmitted to the machine base. Transmitted forces will excite vibrations in machine supports and floors and walls of buildings, and the like, giving rise to additional noise radiation from these other areas.
Chapter 9of this book gives a more complete discussion on vibration isolation.
What is the maximum stiffness of an undamped isolator to provide 80% isolation for a 300‐kg machine operating at 1000 rpm?
The excitation frequency is f = 1000/60 = 16.7 Hz, or ω = 1000 × (2 π /60) = 104.7 rad/s. For 80% isolation the maximum force transmissibility is 0.2.
Using Eq. (2.21)with δ = 0 and noting that isolation only occurs when 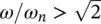 we get that 0.2 ≥ [( ω / ω n) 2− 1] −1which is solved giving ω / ω n≥ 2.45. This result can be also obtained from Figure 2.10. Therefore, the system's maximum allowable natural frequency is f n= 6.8 Hz, or ω n= ω /2.45 = 104.7/2.45 = 42.7 rad/s. Consequently, the maximum isolator stiffness is K = Mω n 2= (300) × (42.7) 2= 5.47 × 10 5N/m.
we get that 0.2 ≥ [( ω / ω n) 2− 1] −1which is solved giving ω / ω n≥ 2.45. This result can be also obtained from Figure 2.10. Therefore, the system's maximum allowable natural frequency is f n= 6.8 Hz, or ω n= ω /2.45 = 104.7/2.45 = 42.7 rad/s. Consequently, the maximum isolator stiffness is K = Mω n 2= (300) × (42.7) 2= 5.47 × 10 5N/m.
2.4 Multi‐Degree of Freedom Systems
Читать дальше

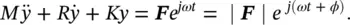

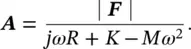
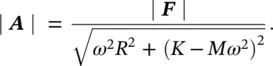
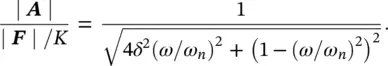

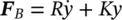 . Substituting this into Eq. (2.17)and rearranging and finally comparing the amplitudes of the imposed force | F| with the force transmitted to the base | F B| gives
. Substituting this into Eq. (2.17)and rearranging and finally comparing the amplitudes of the imposed force | F| with the force transmitted to the base | F B| gives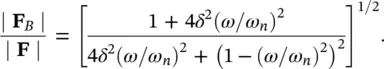

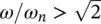 we get that 0.2 ≥ [( ω / ω n) 2− 1] −1which is solved giving ω / ω n≥ 2.45. This result can be also obtained from Figure 2.10. Therefore, the system's maximum allowable natural frequency is f n= 6.8 Hz, or ω n= ω /2.45 = 104.7/2.45 = 42.7 rad/s. Consequently, the maximum isolator stiffness is K = Mω n 2= (300) × (42.7) 2= 5.47 × 10 5N/m.
we get that 0.2 ≥ [( ω / ω n) 2− 1] −1which is solved giving ω / ω n≥ 2.45. This result can be also obtained from Figure 2.10. Therefore, the system's maximum allowable natural frequency is f n= 6.8 Hz, or ω n= ω /2.45 = 104.7/2.45 = 42.7 rad/s. Consequently, the maximum isolator stiffness is K = Mω n 2= (300) × (42.7) 2= 5.47 × 10 5N/m.










