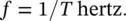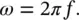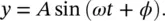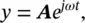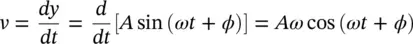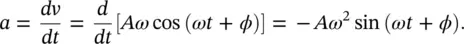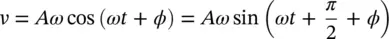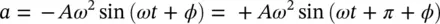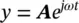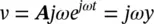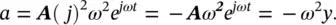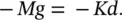Malcolm J. Crocker - Engineering Acoustics

(2.1)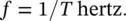

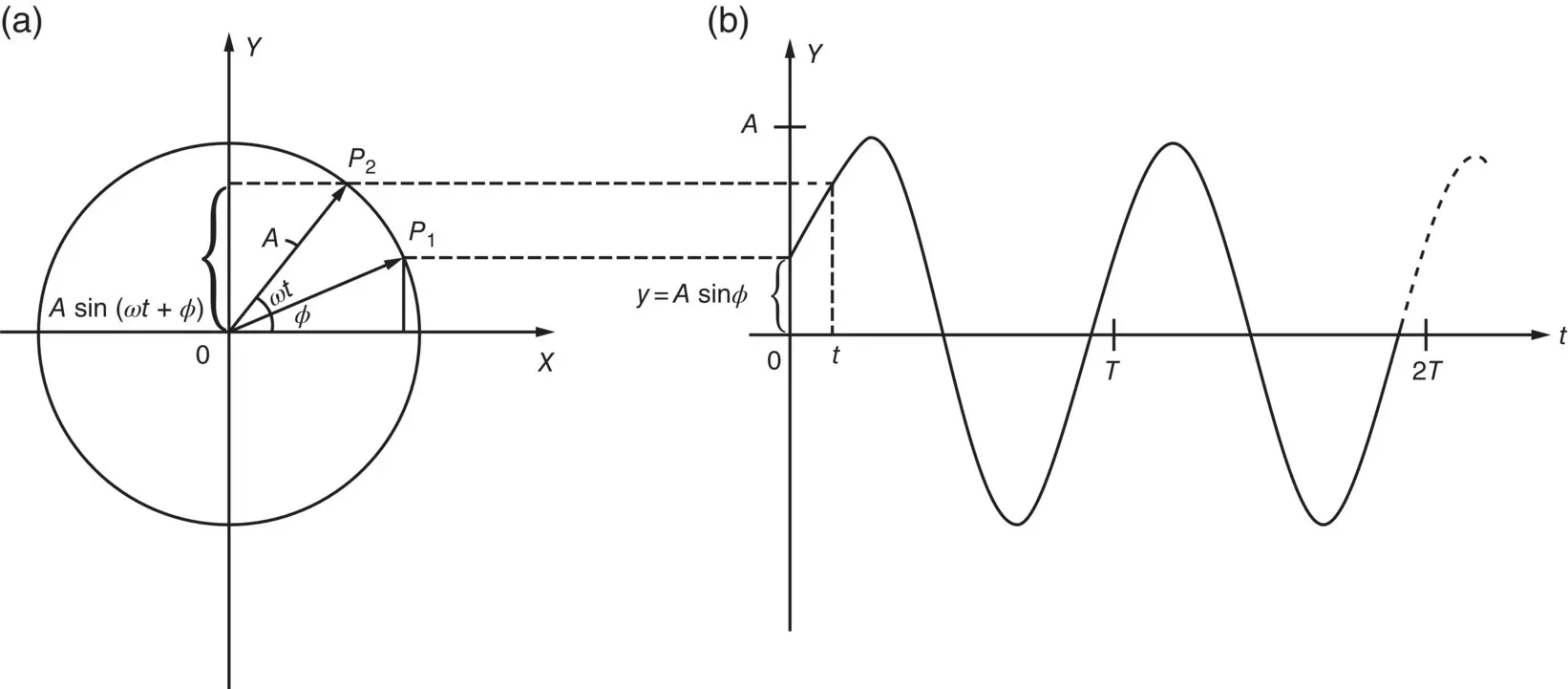
Figure 2.3 Simple harmonic motion with initial phase angle ϕ .

The time T is known as the period and is usually measured in seconds. From Figures 2.2and 2.3, we see that the motion repeats itself every time ωt increases by 2 π , since sin(0) = sin(2 π ) = sin(4 π ) = 0, and so on. Thus ωT = 2 π and from Eq. (2.1),

(2.2)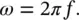

The angular frequency, ω , is expressed in radians per second (rad/s).

The motion described by the displacement y in Figure 2.2or the projection OP on the X‐ or Y‐ axes in Figure 2.2is said to be simple harmonic . We must now discuss something called the initial phase angle , which is sometimes just called phase . For the case we have chosen in Figure 2.2, the phase angle is zero. If, instead, we start counting time from when the vector points in the direction OP 1, as shown in Figure 2.3, and we let the angle XOP 1= ϕ , this is equivalent to moving the time origin t seconds to the right in Figure 2.2. Time is started when P is at P 1and thus the initial displacement is A sin( ϕ ). The initial phase angle is ϕ . After time t , P 1has moved to P 2and the displacement

(2.3)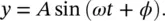

If the initial phase angle ϕ = 0°, then y = A sin( ωt ); if the phase angle ϕ = 90°, then y = A sin( ωt + π /2) = A cos( ωt ). For mathematical convenience, complex exponential notation is often used. If the displacement is written as

(2.3a)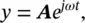

and we remember that A e jωt= A [cos( ωt ) + j sin( ωt )], we see in Figure 2.1that the real part of Eq. (2.3a)is represented by the projection of the point P onto the x ‐axis, A cos( ωt ), and of the point P onto the Y‐ (or imaginary axis), A sin( ωt ). Simple harmonic motion, then, is often written as the real part of A e jωt, or in the more general form y = Ae j(ωt + ϕ). If the constant A is made complex, then the displacement can be written as the real part of y = A e jωt, where A= Ae jϕ.

So far we have examined the displacement y of a point. Note that, when the displacement is in the OY direction, we say it is positive; when it is in the opposite direction to OY , we say it is negative. Displacement, velocity, and acceleration are really vector quantities in mathematics; that is, they have magnitude and direction. The velocity v of a point is the rate of change of position with time of the point x in m/s. The acceleration a is the rate of change of velocity with time. Thus, using simple calculus:

(2.4)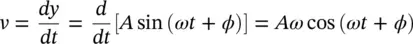

and

(2.5)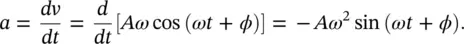

Equations are plotted in Figure 2.4.

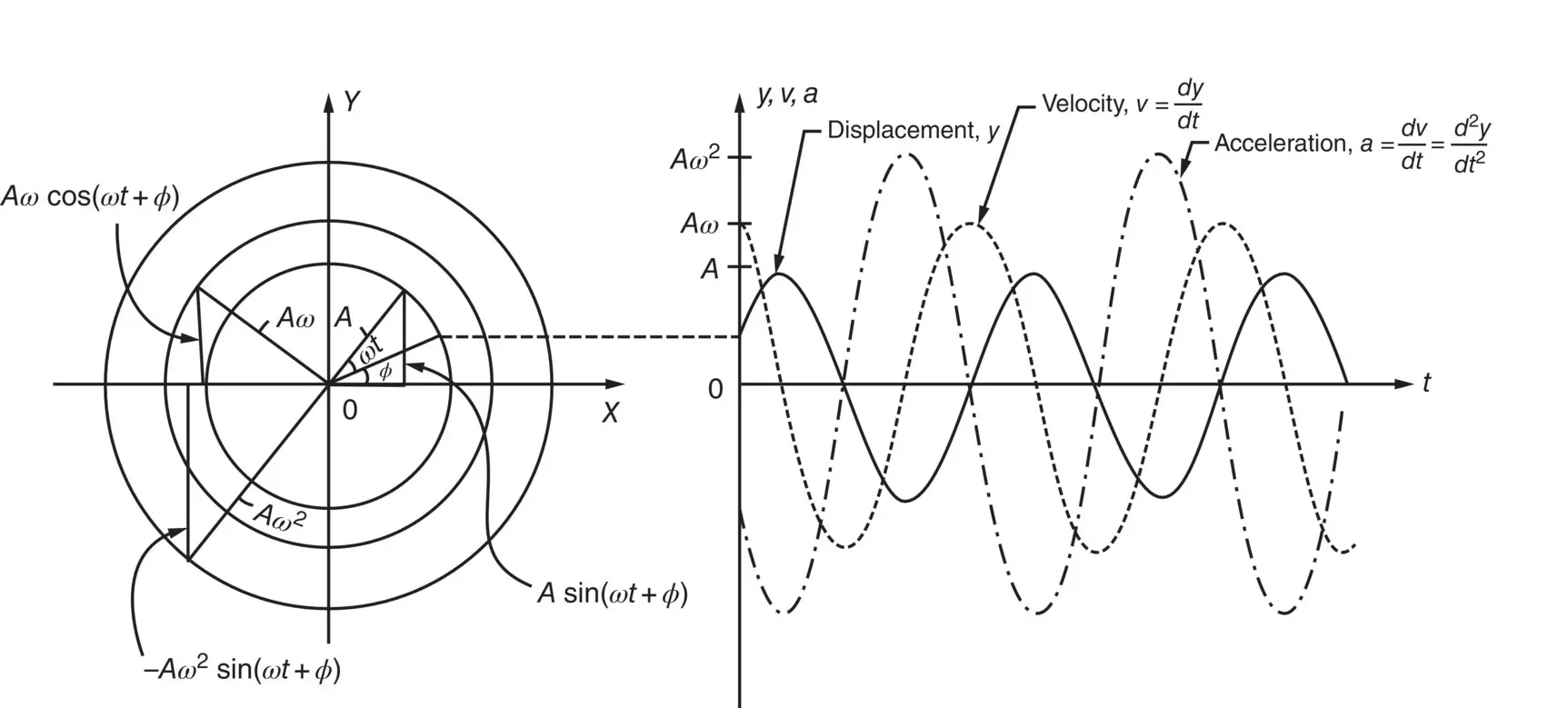
Figure 2.4 Displacement, velocity, and acceleration.

Note, by trigonometric manipulation we can rewrite Eqs. (2.4)and (2.5)as (2.6)and (2.7):

(2.6)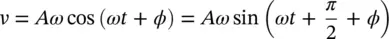

and

(2.7)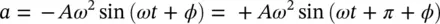

and from Eq. (2.3)we see that a = − ω 2 y .

Equations tell us that for simple harmonic motion the amplitude of the velocity is ω or 2 πf greater than the amplitude of the displacement, while the amplitude of the acceleration is ω 2or (2 πf ) 2greater. The phase of the velocity is π /2 or 90° ahead of the displacement, while the acceleration is π or 180° ahead of the displacement.

Note we could have come to the same conclusions and much more quickly if we had used the complex exponential notation. Writing

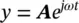
then

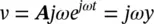
and

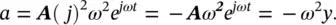
In a simple harmonic motion of frequency 10 Hz, the displacement amplitude is 2 mm. Calculate the maximum velocity amplitude and maximum acceleration amplitude.

Since ω = 2 πf = 2 π (10) = 62.83 rad/s. The velocity amplitude is calculated as

ν = ω × 2 = 62.83 × 2 = 125.7 mm/s and the acceleration amplitude is a = ω 2× 2 = (62.83) 2× 2 = 7896 mm/s 2.

a) Free Vibration – Undamped

Suppose a mass of M kilogram is placed on a spring of stiffness K newton‐metre (see Figure 2.5a), and the mass is allowed to sink down a distance d metres to its equilibrium position under its own weight Mg newtons, where g is the acceleration of gravity 9.81 m/s 2. Taking forces and deflections to be positive upward gives

(2.8)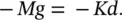

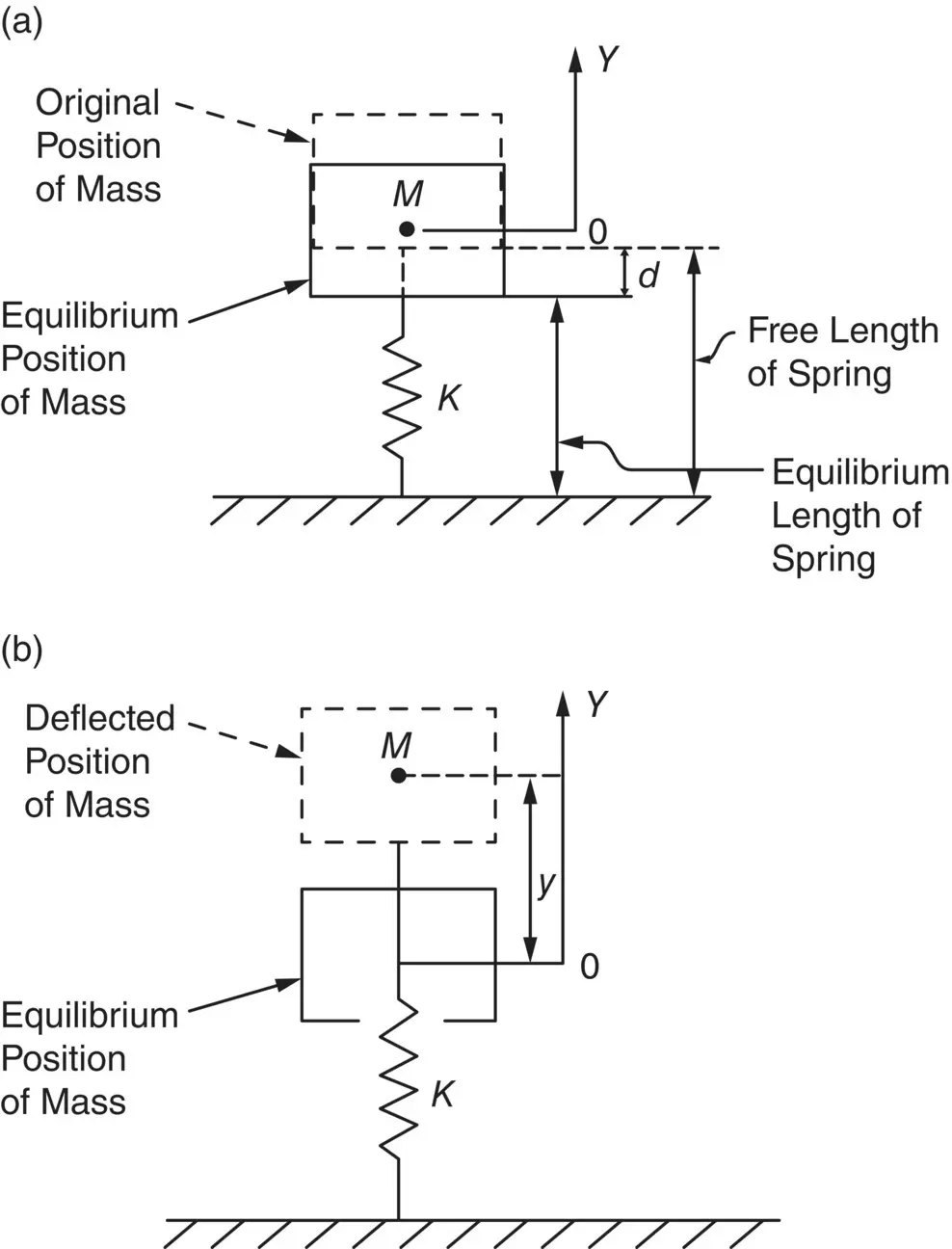
Figure 2.5 Movement of mass on a spring: (a) static deflection due to gravity and (b) oscillation due to initial displacement y 0.