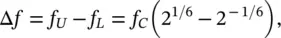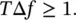a) One‐Octave Bands
For one‐octave bands, the cutoff frequencies f Land f Uare defined as follows:
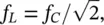
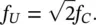
The center frequency (or geometric mean) is 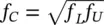 . Thus f U/ f L= 2.
. Thus f U/ f L= 2.
The bandwidth Δ f is given by
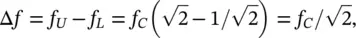
so Δ f ≈ 70% ( f C).
b) One‐Third‐Octave Bands
For one‐third‐octave bands, the cutoff frequencies, f Land f U, are defined as follows:
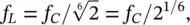
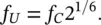
The center frequency (geometric mean) is given by 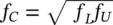 . Thus f U/ f L= 2 1/3.
. Thus f U/ f L= 2 1/3.
The bandwidth Δ f is given by
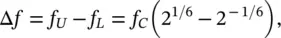
so Δ f ≈ 23% ( f C).
We thus see clearly why the filter bands we have just discussed are called constant percentage. This is because the bandwidth is a constant percentage of the filter center frequency f C. Of course, the filter bandwidth does not have to be defined in terms of a fraction of an octave but can be defined simply in terms of the percentage of the center frequency. Since it is impracticable to make measurements at a large number of fixed frequencies, noise measurements are made at a selected number of standardized frequencies called preferred center frequencies . Standard one-octave and one-third-octave band specifications take advantage of the fact that 2 10/3≈ 10. The ISO recommendation values for preferred center frequencies are given in Table 1.1[15]. Specifications for octave‐band and fractional‐octave‐band filters are defined by the IEC 1260:1995 and the ANSI S1.11:2004 standards [16, 17].
Table 1.1 Preferred center frequencies for noise measurements according to ISO R 266 [15].
| Preferredfrequencies, Hz |
1/1oct. |
1/3oct. |
Preferredfrequencies, Hz |
1/1oct. |
1/3oct. |
Preferredfrequencies, Hz |
1/1oct. |
1/3oct. |
| 16 |
× |
× |
200 |
|
× |
2500 |
|
× |
| 20 |
|
× |
250 |
× |
× |
3150 |
|
× |
| 25 |
|
× |
315 |
|
× |
4000 |
× |
× |
| 31.5 |
× |
× |
400 |
|
× |
5000 |
|
× |
| 40 |
|
× |
500 |
× |
× |
6300 |
|
× |
| 50 |
|
× |
630 |
|
× |
8000 |
× |
× |
| 63 |
× |
× |
800 |
|
× |
10 000 |
|
× |
| 80 |
|
× |
1000 |
× |
× |
12 500 |
|
× |
| 100 |
|
× |
1250 |
|
× |
16 000 |
× |
× |
| 125 |
× |
× |
1600 |
|
× |
|
|
|
| 160 |
|
× |
2000 |
× |
× |
|
|
|
Note that:
1 The center frequencies of one‐octave bands are related by 2, and 10 frequency bands are used to cover the human hearing range. They have center frequencies of 31.5, 63, 125, 250, 500, 1000, 2000, 4000, 8000, 16 000 Hz.
2 The center frequencies of one‐third octave bands are related by 21/3 and 10 cover a decade of frequency, and thus 30 frequency bands are used to cover the human hearing range: 20, 25, 31.5, 40, 50, 63, 80, 100, 125, 160, …, 16 000 Hz.
Thus we note that at high frequencies a constant bandwidth analyzer will obviously have a narrower bandwidth than the constant percentage filter. Figure 1.11shows a comparison of the bandwidths of constant percentage and constant band filters at the same frequencies.
Determine the percentage bandwidth of the center frequency of a 1/12‐octave band filter.
1/12-octave filters are obtained by dividing each one-octave band into 12 geometrically equal sub‐sections, i.e. f U/ f L= 2 1/12. By the same procedure as for octave and one‐third‐octave filters, we get the result that for 1/12‐octave bands the cutoff frequencies, f Land f U, are f C× 2 −1/24and f C× 2 1/24, respectively. Then, the bandwidth is given by Δ f = f U− f L= f C(2 1/24− 2 −1/24), so Δ f ≈ 6% ( f C).
There are two main types of constant percentage filters in common use: (i) those with a fixed center frequency and bandwidth which is a certain percentage of the center frequency, and (ii) those with a variable (or tunable) center frequency and a bandwidth which can be set to certain selected percentages of the center frequency. The first type of filter is perhaps in most common use. In practical instruments, many different parallel filters each with a different center frequency are assembled in one unit. The instrument is provided with a root mean square detector and a display.
On the other hand, instruments for constant bandwidth filter analysis are normally constructed so that the center frequency of a single filter can be tracked effectively throughout the frequency range of interest. Often different bandwidth settings are available on the same instrument (e.g. 1, 5, 10, 20 Hz). The narrower the bandwidth chosen, the slower the tracking rate should be to obtain reliable results. A rule which should be used in spectrum analysis is that the duration, T , of the noise sample length (or of the analysis time) must be at least as long as the reciprocal of the bandwidth Δ f ,
(1.16) 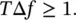
This fundamental principle, also known as the uncertainty principle , puts a limit on the corresponding resolutions in the time and frequency domain, meaning that narrow resolution in one domain means wide resolution in the other domain [10].
If fine frequency resolution is not needed or if the signal is broadband in nature, then octave band readings are sufficient. One‐third octave band readings (or narrower) should be used if the signal spectrum is not smooth or if pure tones are present. For diagnostic work on machinery, it may be necessary to use constant bandwidth filters (e.g. if the fan blade passing frequency and its higher harmonics must be separated).
Читать дальше

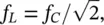
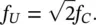
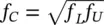 . Thus f U/ f L= 2.
. Thus f U/ f L= 2.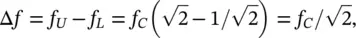
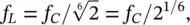
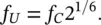
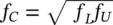 . Thus f U/ f L= 2 1/3.
. Thus f U/ f L= 2 1/3.